题目内容
13.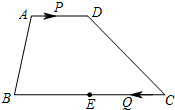 如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t为多少秒时,以点P,Q,E,D为顶点的四边形是平行四边形?
如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t为多少秒时,以点P,Q,E,D为顶点的四边形是平行四边形?
分析 由已知以点P,Q,E,D为顶点的四边形是平行四边形有两种情况,(1)当Q运动到E和B之间,(2)当Q运动到E和C之间,根据平行四边形的判定,由AD∥BC,所以当PD=QE时为平行四边形.根据此设运动时间为t,列出关于t的方程求解.
解答 解:由已知梯形,
当Q运动到E和B之间,设运动时间为t,则得:
2t-$\frac{16}{2}$=6-t,
解得:t=$\frac{14}{3}$,
当Q运动到E和C之间,设运动时间为t,则得:$\frac{16}{2}$-2t=6-t,
解得:t=2,
故当运动时间t为2或$\frac{14}{3}$秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
点评 此题主要考查了梯形及平行四边形的性质,关键是由已知明确有两种情况,不能漏解.

练习册系列答案
相关题目
4.计算(-2a2)3的结果是( )
| A. | 2a4 | B. | -2a4 | C. | 8a6 | D. | -8a6 |
2.“4的平方根是±2”用数学式子表示为( )
| A. | $\sqrt{4}$=±2 | B. | ±$\sqrt{4}$=±2 | C. | ±$\sqrt{4}$=2 | D. | $\sqrt{4}$=±2 |
 已知:如图,AB∥CD,∠B=35°,∠1=75°.求∠A的度数.解题思路分析:欲求∠A,只要求∠ACD的大小.
已知:如图,AB∥CD,∠B=35°,∠1=75°.求∠A的度数.解题思路分析:欲求∠A,只要求∠ACD的大小.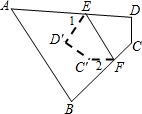 如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.
如图,将四边形ABCD纸片沿EF折叠,使点C、D落在四边形ABFE内点C′、D′的位置,∠A=50°,∠B=70°,则∠1+∠2=120度.