题目内容
12.如图1,在△ABC汇总,∠ACB=2∠B,射线AO平分∠BAC交BC于点D,点M是直线BC上的动点,过点M作直线l⊥AO于H,分别交射线AB、AC于点N、E.(1)若∠BAC=90°,且当M与点C重合时(如图2),请直接写出线段BN与CD的数量关系;
(2)若∠BAC≠90°,且当M与点C重合时(如图3),判断(1)题的结论是否成立?若成立,请证明;若不成立,说明理由;
(3)在直线l随点M运动的过程中,探究线段BN、CE、CD之间的等量关系,并直接写出结论.
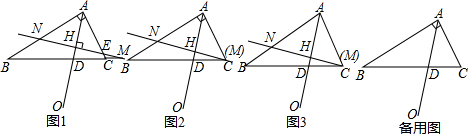
分析 (1)连接ND,先由已知条件证明:DN=DC,再证明BN=DN即可;
(2)连结ND,易证AN=AC,易证∠B=∠BDN,可得BN=DN,即可解题;
(3)BN、CE、CD之间的等量关系要分三种情况讨论:①当点M在线段BC上时;②当点M在BC的延长线上时;③当点M在CB的延长线上时.
解答 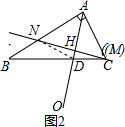 解:(1)证明:如图2,连结ND,
解:(1)证明:如图2,连结ND,
∵AO平分∠BAC,
∴∠BAD=∠CAD,
∵直线l⊥AO于H,
∴∠AHN=∠AHE=90°,
∴∠ANH=∠AEH,
∴AN=AC,
∴NH=CH,
∴AH是线段NC的中垂线
∴DN=DC,
∴∠DNH=∠DCH,
∴∠AND=∠ACB,
∵∠AND=∠B+∠BDN,∠ACB=2∠B,
∴∠B=∠BDN,
∴BN=DN,
∴BN=DC;
(2)证明:如图3,连结ND,
,∵AO平分∠BAC,
∴∠BAD=∠CAD,
∵直线l⊥AO于H,
∴∠AHN=∠AHE=90°,
∴∠ANH=∠AEH,
∴AN=AC,
∴NH=CH,
∴AH是线段NC的中垂线
∴DN=DC,
∴∠DNH=∠DCH,
∴∠AND=∠ACB,
∵∠AND=∠B+∠BDN,∠ACB=2∠B,
∴∠B=∠BDN,
∴BN=DN,
∴BN=DC;
(3)解:如图4,BN、CE、CD之间的等量关系:
①过C作CG∥AB,CN′∥GN,
∴四边形NN′CG是平行四边形,
∴NN′=CG,
∴∠BNM=∠CGM,
∴∠ANM=∠CGE,∵∠ANM=∠E,
∴∠CGE=∠E,
∴CG=CE,
∴NN′=CE,
在△ANH与△AEH中,$\left\{\begin{array}{l}{∠NAH=∠EAH}\\{AH=AH}\\{∠AHN=∠AHE=90°}\\{\;}\end{array}\right.$,
∴AN=AE,
由(1)证得:BN′=CD,
∴CD=BN+CE,
②当点M在BC的延长线上时,过C作CG∥AB,CN′∥GN,
∴四边形NN′CG是平行四边形,
∴NN′=CG,
∴∠BNM=∠CGM,
∴∠ANM=∠CGE,
∵∠ANM=∠E,
∴∠CGE=∠E,
∴CG=CE,
∴NN′=CE,
在△ANH与△AEH中,$\left\{\begin{array}{l}{∠NAH=∠EAH}\\{AH=AH}\\{∠AHN=∠AHE=90°}\\{\;}\end{array}\right.$,
∴AN=AE,
由(1)证得:BN′=CD,
∴CD=BN-CE;
③当点M在CB的延长线上时,过C作CG∥AB,CN′∥GN,
∴四边形NN′CG是平行四边形,
∴NN′=CG,
∴∠BNM=∠CGM,
∴∠ANM=∠CGE,
∵∠ANM=∠E,
∴∠CGE=∠E,
∴CG=CE,
∴NN′=CE,
在△ANH与△AEH中,$\left\{\begin{array}{l}{∠NAH=∠EAH}\\{AH=AH}\\{∠AHN=∠AHE=90°}\\{\;}\end{array}\right.$,
∴AN=AE,
由(1)证得:BN′=CD,
∴CD=CE-BN.
点评 本题考查了线段垂直平分线的判定和性质,考查了全等三角形对应边相等的性质,考查了等腰三角形底边三线合一的性质,本题中证得AH垂直平分NE是解题的关键.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案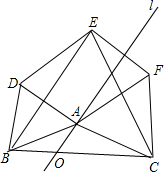 如图,已知线段BC=6,O为线段BC上一点,且OB=2,过O点的直线l与BC的夹角是60°,A为l上的一个动点,分别以AC,BC为边在BC的同侧作等边△ABD,△ACF,△BCE,连接EF,则平行四边形,菱形,矩形,线段,等腰梯形中符合以点A,D,E,F构成的图形有( )
如图,已知线段BC=6,O为线段BC上一点,且OB=2,过O点的直线l与BC的夹角是60°,A为l上的一个动点,分别以AC,BC为边在BC的同侧作等边△ABD,△ACF,△BCE,连接EF,则平行四边形,菱形,矩形,线段,等腰梯形中符合以点A,D,E,F构成的图形有( )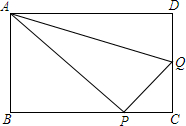 如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P从B点开始沿边BC向点C以4cm/s的速度运动,同时动点Q从C点开始沿边CD向点D以1cm/s的速度运动,当其中一个到达终点时,另一个也随之停止运动.
如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P从B点开始沿边BC向点C以4cm/s的速度运动,同时动点Q从C点开始沿边CD向点D以1cm/s的速度运动,当其中一个到达终点时,另一个也随之停止运动. 如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=$\frac{1}{2}$x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=$\frac{1}{2}$x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).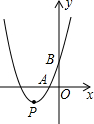 如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=$\frac{1}{3}$.
如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=$\frac{1}{3}$. 如图,己知∠1=∠2,AC=AD,增加一个条件能使△ABC≌△AEDAB=AE.
如图,己知∠1=∠2,AC=AD,增加一个条件能使△ABC≌△AEDAB=AE.