题目内容
20. 如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E.
如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E.(1)求证:AD=AE.
(2)连结CA,若∠DCA=70°,求∠CAE的度数.
分析 (1)由等腰三角形的性质和矩形的性质证出∠FCA=∠DCA,由AAS证明△ADC≌△CAE,即可得出结论;
(2)由全等三角形的性质得出∠CAE=∠CAD,求出∠CAD=90°-∠DCA=20°,即可得出答案.
解答 (1)证明:连接AC,如图所示: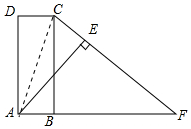
∵CF=AF,∴∠FCA=∠CAF,
∵四边形ABCD是矩形,∴DC∥AB∴,∠DCA=∠CAF,
∴∠FCA=∠DCA,
∵AE⊥FC,
∴∠CEA=90°,
∴∠CDA=∠CEA=90°,
在△ADC和△CAE 中,$\left\{\begin{array}{l}{∠CDA=∠CEA}&{\;}\\{∠DCA=∠FCA}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ADC≌△CAE (AAS),
∴AD=AE;
(2)解:∵△ADC≌△CAE,
∴∠CAE=∠CAD,
∵四边形ABCD是矩形,
∴∠D=90°,
∴∠CAD=90°-∠DCA=90°-70°=20°,
∴∠CAE=20°.
点评 此题主要考查了全等三角形的判定与性质,矩形的性质、等腰三角形的性质、平行线的性质等知识;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
11.已知,二次函数y=x2+bx-2017的图象与x轴交于点A(x1,0)、B(x2,0)两点,则当x=x1+x2时,则y的值为( )
| A. | 2019 | B. | 2017 | C. | 2018 | D. | -2017 |
12.新学期开学了,文具店张经理购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
(1)张经理如何进货,才能使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮张经理设计一个进货方案,并求出其所获利润的最大值.
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮张经理设计一个进货方案,并求出其所获利润的最大值.
4. PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从南京市2016年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从南京市2016年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:
(1)求出表中m,n,a的值,并将条形图补充完整;
(2)以这25天的PM2.5日均值来估计该年的空气质量情况,估计该年(365天)大约有多少天的空气质量达到优或良.
 PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从南京市2016年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从南京市2016年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:| 空气质量等级 | PM2.5日均值标准值 | 频数 | 频率 |
| 优 | 0-35 | 1 | 0.04 |
| 良 | 35-75 | m | 0.2 |
| 轻度污染 | 75-150 | 11 | 0.44 |
| 中度污染 | 150-200 | 5 | 0.2 |
| 重度污染 | 200-300 | n | a |
| 严重污染 | 大于300 | 1 | 0.04 |
(2)以这25天的PM2.5日均值来估计该年的空气质量情况,估计该年(365天)大约有多少天的空气质量达到优或良.
 如图,有一块四边形空地ABCD,AB=3cm,BC=4cm,CD=12cm,DA=13cm,∠B=90°.现要在空地处种植草坪,求草坪的种植面积.
如图,有一块四边形空地ABCD,AB=3cm,BC=4cm,CD=12cm,DA=13cm,∠B=90°.现要在空地处种植草坪,求草坪的种植面积. 如图所示,某小区一栋新建住宅楼AB正前方有一栋高度是10米的旧楼房ED,从新楼顶端A处测得在其正前方的旧楼的顶端E的仰角是30°,旧楼底端D到新楼前梯坎底边的距离DC是10$\sqrt{3}$米,梯坎坡长BC是8米,梯坎坡度i=1:$\sqrt{3}$,春节期间居委会想在AE之间悬挂一条彩带来烘托节日气氛,求这条彩带的长度和新建住宅楼AB的高度.
如图所示,某小区一栋新建住宅楼AB正前方有一栋高度是10米的旧楼房ED,从新楼顶端A处测得在其正前方的旧楼的顶端E的仰角是30°,旧楼底端D到新楼前梯坎底边的距离DC是10$\sqrt{3}$米,梯坎坡长BC是8米,梯坎坡度i=1:$\sqrt{3}$,春节期间居委会想在AE之间悬挂一条彩带来烘托节日气氛,求这条彩带的长度和新建住宅楼AB的高度.