题目内容
10．已知（x-15）2+$\sqrt{17-y}$+z2-16z+64=0，试判断以x，y，z为三边的三角形的形状．分析 先根据非负数的性质求出x、y、z的值，再根据勾股定理的逆定理进行解答即可．
解答 解：以x，y，z为三边的三角形是直角三角形．
∵（x-15）2+$\sqrt{17-y}$+z2-16z+64=0，
∴（x-15）2+$\sqrt{17-y}$+（z-8）2=0，
∴x-15=0，17-y=0，z-8=0，
∴x=15，y=17，z=8，
∵152+82=172，
∴以x，y，z为三边的三角形是直角三角形．
点评 本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
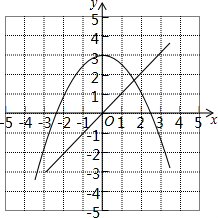我们在求方程x2+2x-6=0的近似根时，可以将原方程变形为-$\frac{1}{2}$x2+3=x，然后在同一直角坐标系中画出函数y=-$\frac{1}{2}$x2+3和y=x的图象，发现-4＜x1＜-3，1＜x2＜2．请你利用已有的函数图象判断方程x3-6x+12=0在实数范围内有几个解？
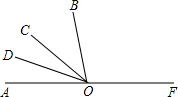如图，已知O为直线AF上一点，射线OC平分∠AOB，∠COD=20°；