题目内容
20. 某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.
某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程如下:
甲:12x+8(20-x)=180;乙:$\frac{x}{12}$+$\frac{180-x}{8}$=20.
根据甲、乙两名同学所列的方程,请你分别指出代数式表示的意义.
甲:x表示A工程队用的时间,20-x表示20-x表示B工程队用的时间;
乙:x表示A工程队整治河堤的米数,180-x表示B工程队整治河堤的米数.
(2)请你从甲、乙两位同学的解答思路中,选择一种你喜欢的思路,求A、B两工程队分别整治河堤的长度.写出完整的解答过程.
分析 (1)根据所列方程可得第一个方程为12x+8(20-x)=180,x表示A工程队用的时间,20-x表示B工程队用的时间;
第二个方程为$\frac{x}{12}$+$\frac{180-x}{8}$=20,x表示A工程队整治河堤的米数,表示B工程队整治河堤的米数;
(2)求解第一个方程即可.
解答 解:(1)由题意得,第一个方程为12x+8(20-x)=180,x表示A工程队用的时间,20-x表示B工程队用的时间;
第二个方程为$\frac{x}{12}$+$\frac{180-x}{8}$=20,x表示A工程队整治河堤的米数,180-x表示B工程队整治河堤的米数;
故答案为:A工程队用的时间,20-x表示B工程队用的时间;A工程队整治河堤的米数,B工程队整治河堤的米数;
(2)设A工程队用的时间为x天,
根据题意,得12x+8(20-x)=180,
解得:x=5,
12x=12×5=60,8(20-x)=8×(20-5)=120,
答:A工程队整治河堤60数,B工程队整治河堤120米.
点评 本题考查了一元一次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
13.把直线y=3x-4沿x轴的正方向平移4个单位,得到的直线解析式为( )
| A. | y=3x | B. | y=3x-8 | C. | y=3x-16 | D. | y=3x+12 |
11. 有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.
有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.
 有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.
有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.| A. | 64 | B. | 52 | C. | 38 | D. | 26 |
5.一元二次方程x2-3x+3=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 不能确定 |
10.用科学记数法表示0.000 000 000 000 002 56为( )
| A. | 0.256×10-14 | B. | 2.56×10-15 | C. | 0.256×10-15 | D. | 256×10-17 |
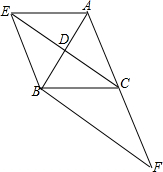 已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.
已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.