题目内容
12．一次函数y=$\frac{5}{4}$x+5的图象与x轴y轴分别交于A点，B点，则这两点间的距离为$\sqrt{41}$．分析 先求出A、B两点的坐标，再利用两点间的距离公式进行解答即可．
解答 解：令x=0，则y=5；
令y=0，则x=-4，
∵A、B两点分别是一次函数y=x+3的图象与x轴、y轴的公共点，
∴A（-4，0）、B（0，5），
∴AB=$\sqrt{（-4-0）^{2}+（5-0）^{2}}$=$\sqrt{41}$．
故答案为：$\sqrt{41}$．
点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上点的坐标特点及两点间的距离公式是解答此题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
2．根据下表中一次函数的自变量x和函数y的对应值，m的值为3．
| x | -1 | 0 | 1 |
| y | 7 | 5 | m |
已知一次函数y=kx+b的图象经过点A（1，3）和B（-1，-1）两点．
7．
如图，在△ABC中，AD平分∠BAC，按如下步骤作图：
步骤1：分别以点A，D为圆心，以大于$\frac{1}{2}$AD的长为半径，在AD两侧作弧，两弧交于点M，N；
步骤2：连接MN，分别交AB，AC于点E，F；
步骤3：连接DE，DF．
下列叙述不一定成立的是（ ）
如图，在△ABC中，AD平分∠BAC，按如下步骤作图：步骤1：分别以点A，D为圆心，以大于$\frac{1}{2}$AD的长为半径，在AD两侧作弧，两弧交于点M，N；
步骤2：连接MN，分别交AB，AC于点E，F；
步骤3：连接DE，DF．
下列叙述不一定成立的是（ ）
| A． | 线段DE是△ABC的中位线 | B． | 四边形AFDE是菱形 | ||
| C． | MN垂直平分线段AD | D． | $\frac{BD}{DC}$=$\frac{BE}{EA}$ |
已知矩形ABCD的长AB=2，AB边与x轴重合，双曲线y=$\frac{k}{x}$在第一象限内经过D点以及BC的中点E．
4．
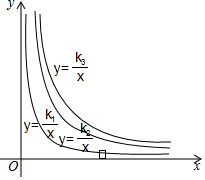甲、乙、丙三人直立在相同大小的平板上，平板对水平地面的压强y（帕）与平板面积x（m）的关系分别如图中的y=$\frac{{k}_{1}}{x}$，y=$\frac{{k}_{2}}{x}$，y=$\frac{{k}_{3}}{x}$，则当平板面积增加量相同时，甲、乙、丙三人所站的平板对水平地面的压强变化的关系是（ ）
甲、乙、丙三人直立在相同大小的平板上，平板对水平地面的压强y（帕）与平板面积x（m）的关系分别如图中的y=$\frac{{k}_{1}}{x}$，y=$\frac{{k}_{2}}{x}$，y=$\frac{{k}_{3}}{x}$，则当平板面积增加量相同时，甲、乙、丙三人所站的平板对水平地面的压强变化的关系是（ ）| A． | 甲的压强增加量＞乙压强增加量＞乙压强增加量 | |
| B． | 甲的压强减少量＞乙压强减少量＞乙压强减少量 | |
| C． | 乙的压强减少量＞甲压强减少量＞丙的压强减少量 | |
| D． | 丙的压强减少量＞乙压强减少量＞甲压强减少量 |
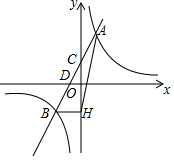一次函数y=ax+b（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象相交于A，B两点，与y轴交于点C，与x轴交于点D，点D的坐标为（-1，0），点A的横坐标是1，tan∠CDO=2．过点B作BH⊥y轴交y轴于H，连接AH．