题目内容
18.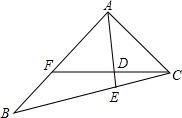 如图,△ABC中,点F在边AB上,AC=AF,AD⊥CF于点D,AD的延长线交BC于点E,求证:$\frac{BE}{EC}$=$\frac{AB}{AF}$.
如图,△ABC中,点F在边AB上,AC=AF,AD⊥CF于点D,AD的延长线交BC于点E,求证:$\frac{BE}{EC}$=$\frac{AB}{AF}$.
分析 过C作CG∥AB交AE的延长线于G,得到△ABE∽△GCE,证得$\frac{BE}{CE}=\frac{AB}{CG}$,根据等腰三角形的性质得到∠FAD=∠CAD,推出AC=CG,等量代换得到结论.
解答  证明:过C作CG∥AB交AE的延长线于G,
证明:过C作CG∥AB交AE的延长线于G,
∴△ABE∽△GCE,
∴$\frac{BE}{CE}=\frac{AB}{CG}$,
∵AC=AF,AD⊥CF,
∴∠FAD=∠CAD,
∵CG∥AB,
∴∠BAG=∠G,
∴∠CAD=∠G,
∴AC=CG,
∴CG=AF,
∴$\frac{BE}{EC}$=$\frac{AB}{AF}$.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
相关题目
3.在解方程$\frac{x+1}{2}$+$\frac{x-1}{3}$=1时,去分母正确的是( )
| A. | 3x+1-2x-1=1 | B. | 3x+1-2x-1=6 | C. | 3(x+1)+2(x-1)=6 | D. | 3(x+1)-2(x-1)=1 |
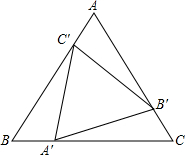 已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.
已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.