题目内容
14.正n边形的边长与半径之比是( )| A. | 2cos$\frac{180°}{n}$ | B. | 2sin$\frac{180°}{n}$ | C. | 2tan$\frac{180°}{n}$ | D. | 2cot$\frac{180°}{n}$ |
分析 根据题意可以求得n边形的每个中心角的度数,从而可以表示出正n边形的边长与半径,从而可以求得正n边形的边长与半径之比.
解答 解:设正n边形的边长为x,
则正n边形的每个中心角是$\frac{360°}{n}$,
∴正n边形的半径是:$\frac{\frac{x}{2}}{sin\frac{180°}{n}}$,
∴正n边形的边长与半径之比是:$\frac{x}{\frac{\frac{x}{2}}{sin\frac{180°}{n}}}$=2sin$\frac{180°}{n}$,
故选B.
点评 本题考查正多边形和圆,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
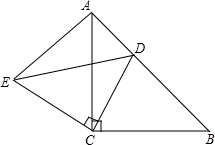 如图,已知△ABC是等腰直角三角形,∠ACB=90°且AB=12cm,点D为AB边上一动点(点D不与点A、B重合).连结CD,以CD为腰向上作等腰直角△CDE,且∠DCE=90°.
如图,已知△ABC是等腰直角三角形,∠ACB=90°且AB=12cm,点D为AB边上一动点(点D不与点A、B重合).连结CD,以CD为腰向上作等腰直角△CDE,且∠DCE=90°.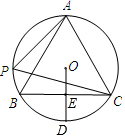 如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.
如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°. 已知△ABC中,∠ABC=40°,∠ACB=80°,O、I、H分别是△ABC的外心、内心和垂心,求证:
已知△ABC中,∠ABC=40°,∠ACB=80°,O、I、H分别是△ABC的外心、内心和垂心,求证: