题目内容
4.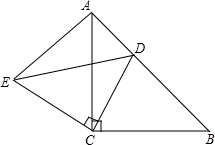 如图,已知△ABC是等腰直角三角形,∠ACB=90°且AB=12cm,点D为AB边上一动点(点D不与点A、B重合).连结CD,以CD为腰向上作等腰直角△CDE,且∠DCE=90°.
如图,已知△ABC是等腰直角三角形,∠ACB=90°且AB=12cm,点D为AB边上一动点(点D不与点A、B重合).连结CD,以CD为腰向上作等腰直角△CDE,且∠DCE=90°.(1)填空:∠BAC=45度;
(2)探索:
①随着点D的移动,四边形AECD面积是否发生变化?若变化,请说出它如何变化;若不变,请求出它的定值;
②当AD为多少时,△ADE的面积有最大值,并求出它的最大值.
分析 (1)根据等腰直角三角形的性质解答;
(2)①证明△ECA≌△DCB,得到四边形AECD面积=△ACB的面积,计算即可;
②设AD=x,根据全等三角形的性质用x表示出BD,根据三角形的面积公式求出△ADE的面积的解析式,根据二次函数的性质解答即可.
解答 解:(1)∵△ABC是等腰直角三角形,∠ACB=90°,AB=12cm,
∴AC=BC=6$\sqrt{2}$cm,
∴△ACB的面积=$\frac{1}{2}$×AC×BC=36cm2,
∴∠BAC=∠B=45°,
故答案为:45;
(2)①∵△ABC是等腰直角三角形,∠ACB=90°,
∵∠ACB=90°,∠DCE=90°,
∴∠ECA=∠DCB,
在△ECA和△DCB中,
$\left\{\begin{array}{l}{EC=DC}\\{∠ECA=∠DCB}\\{AC=BC}\end{array}\right.$,
∴△ECA≌△DCB,
∴四边形AECD面积=△ACB的面积=36cm2,
即四边形AECD面积为定值36cm2;
②∵△ECA≌△DCB,
∴AE=DB,∠EAC=∠B=45°,
∴∠EAD=90°,
设AD=x,则AE=DB=12-x,
△ADE的面积=$\frac{1}{2}$×AE×AD=$\frac{1}{2}$x×(12-x)=$-\frac{1}{2}$(x-6)2+18,
∴当AD为6时,△ADE的面积有最大值,它的最大值是18.
点评 本题考查的是等腰直角三角形的性质、全等三角形的判定和性质、二次函数的解析式的确定以及性质的应用,掌握全等三角形的判定定理和性质定理、正确列出二次函数的解析式是解题的关键.

练习册系列答案
相关题目
14. 已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )
已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )
 已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )
已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )| A. | AB2=AC2+BC2 | B. | BC2=AC•BA | C. | AC2=AB•BC | D. | AC=2BC |
14.正n边形的边长与半径之比是( )
| A. | 2cos$\frac{180°}{n}$ | B. | 2sin$\frac{180°}{n}$ | C. | 2tan$\frac{180°}{n}$ | D. | 2cot$\frac{180°}{n}$ |
 如图,二次函数y=-x2+2x+m+1的图象交x轴于点A(a,0)和B(b,0),交y轴于点C,图象的顶点为D.下列四个命题:
如图,二次函数y=-x2+2x+m+1的图象交x轴于点A(a,0)和B(b,0),交y轴于点C,图象的顶点为D.下列四个命题: 如图所示,AB∥CD,∠CFE的平分线与∠EGB平分线的反向延长线交于点P,若∠E=20°,则∠FPH的度数为多少?
如图所示,AB∥CD,∠CFE的平分线与∠EGB平分线的反向延长线交于点P,若∠E=20°,则∠FPH的度数为多少? 如图,在平面直角坐标系中,有抛物线y=ax2+bx+3,已知OA=OC=3OB,动点P在过A、B、C三点的抛物线上.
如图,在平面直角坐标系中,有抛物线y=ax2+bx+3,已知OA=OC=3OB,动点P在过A、B、C三点的抛物线上.