题目内容
在直角坐标系xOy中,一次函数y=
x+1的图象与二次函数y=-x2+
x+1的图象交于点A、B,则锐角∠ABO的正弦值等于( )
| 1 |
| 2 |
| 9 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:二次函数的性质
专题:计算题
分析:通过解方程组
得A(0,1),B(4,3),如图,作AC⊥OB于C,则可根据勾股计算出OB=5,接着利用面积法求出AC=
,再在Rt△AOC中利用勾股定理计算出OC=
,则BC=OB-OC=
,然后在Rt△ABC中利用正切的定义求解.
|
| 4 |
| 5 |
| 3 |
| 5 |
| 22 |
| 5 |
解答:解:解方程组
得
或
,
则A(0,1),B(4,3),
如图,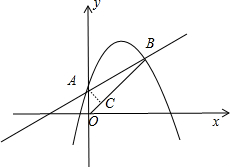 作AC⊥OB于C,
作AC⊥OB于C,
OB=
=5,
△OBA的面积=
×1×4=2,
所以
AC•OB=2,即AC=
,
在Rt△AOC中,OC=
=
,
则BC=OB-OC=5-
=
,
在Rt△ABC中,tan∠ABC=
=
=
,
即锐角∠ABO的正弦值等于
.
故选D.
|
|
|
则A(0,1),B(4,3),
如图,
 作AC⊥OB于C,
作AC⊥OB于C,OB=
| 42+32 |
△OBA的面积=
| 1 |
| 2 |
所以
| 1 |
| 2 |
| 4 |
| 5 |
在Rt△AOC中,OC=
| OA2-AC2 |
| 3 |
| 5 |
则BC=OB-OC=5-
| 3 |
| 5 |
| 22 |
| 5 |
在Rt△ABC中,tan∠ABC=
| AC |
| BC |
| ||
|
| 2 |
| 11 |
即锐角∠ABO的正弦值等于
| 2 |
| 11 |
故选D.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
.也考查了二次函数图象与一次函数图象的交点问题和解直角三角形.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |

练习册系列答案
相关题目
 如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )| A、3cm | B、6cm |
| C、11cm | D、14cm |
 如图,已知AB的长度是a cm,线段BC的长度比线段AB的2倍多5cm,线段AD的长比线段BC长度的2倍少5cm.
如图,已知AB的长度是a cm,线段BC的长度比线段AB的2倍多5cm,线段AD的长比线段BC长度的2倍少5cm.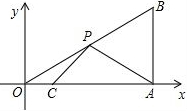 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为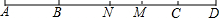 如图,AC=BD,BC:AD=5:9,M是BD的中点.
如图,AC=BD,BC:AD=5:9,M是BD的中点. “宿松家乐福超市”以每件20元的价格进购一批商品,试销一阶段后发现,该商品每天的销售量y(件)与售价x(元/件)之间的函数关系如图(20≤x≤60):
“宿松家乐福超市”以每件20元的价格进购一批商品,试销一阶段后发现,该商品每天的销售量y(件)与售价x(元/件)之间的函数关系如图(20≤x≤60): 如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.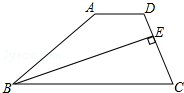 如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )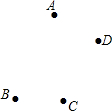 作图题:已知平面上点A,B,C,D.按下列要求画出图形:
作图题:已知平面上点A,B,C,D.按下列要求画出图形: