题目内容
 如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=| 3 |
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
考点:切线的判定,扇形面积的计算
专题:
分析:(1)求出∠COB的度数,求出∠A的度数,根据三角形的内角和定理求出∠OCA的度数,根据切线的判定推出即可;
(2)如解答图所示,解题关键是证明△CDM≌△OBM,从而得到S阴影=S扇形BOC
(2)如解答图所示,解题关键是证明△CDM≌△OBM,从而得到S阴影=S扇形BOC
解答:(1)证明:如图所示: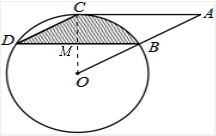 连接OC与BD交于点M.
连接OC与BD交于点M.
根据圆周角定理得:∠COB=2∠CDB=2×30°=60°,
∵AC∥BD,
∴∠A=∠OBD=30°,
∴∠OCA=180°-30°-60°=90°,
即OC⊥AC,
∵OC为半径,
∴AC是⊙O的切线;
(2)解:由(1)知,AC为⊙O的切线,
∴OC⊥AC.
∵AC∥BD,
∴OC⊥BD.
由垂径定理得:MD=MB=
BD=
,
在Rt△OBM中,∠COB=60°,
∴OB=
=
=1,
在△CDM和△OBM中,
∴△CDM≌△OBM(ASA),
∴S△CDM=S△OBM,
∴阴影部分的面积S阴影=S扇形BOC=
=
 连接OC与BD交于点M.
连接OC与BD交于点M.根据圆周角定理得:∠COB=2∠CDB=2×30°=60°,
∵AC∥BD,
∴∠A=∠OBD=30°,
∴∠OCA=180°-30°-60°=90°,
即OC⊥AC,
∵OC为半径,
∴AC是⊙O的切线;
(2)解:由(1)知,AC为⊙O的切线,
∴OC⊥AC.
∵AC∥BD,
∴OC⊥BD.
由垂径定理得:MD=MB=
| 1 |
| 2 |
| ||
| 2 |
在Rt△OBM中,∠COB=60°,
∴OB=
| MB |
| cos30° |
| ||||
|
在△CDM和△OBM中,
|
∴△CDM≌△OBM(ASA),
∴S△CDM=S△OBM,
∴阴影部分的面积S阴影=S扇形BOC=
| 60π•12 |
| 360 |
| π |
| 6 |
点评:本题考查了平行线性质、切线的性质、扇形的面积、三角形的面积、圆周角定理的应用;主要考查学生综合运用定理进行推理和计算的能力.

练习册系列答案
相关题目
 小明玩数学游戏,利用四张完全相同的小长方形纸板测量一张正方形纸板的边长,将它们如图放置,测量的数据如图,则这张正方形纸板的边长为( )
小明玩数学游戏,利用四张完全相同的小长方形纸板测量一张正方形纸板的边长,将它们如图放置,测量的数据如图,则这张正方形纸板的边长为( )| A、60cm | B、70cm |
| C、80cm | D、90cm |
 如图,已知AB的长度是a cm,线段BC的长度比线段AB的2倍多5cm,线段AD的长比线段BC长度的2倍少5cm.
如图,已知AB的长度是a cm,线段BC的长度比线段AB的2倍多5cm,线段AD的长比线段BC长度的2倍少5cm. 如图,线段AB=10cm,C是线段AB上任意一点,M,N分别是AC,BC的中点,“AM=4cm,BN的长为
如图,线段AB=10cm,C是线段AB上任意一点,M,N分别是AC,BC的中点,“AM=4cm,BN的长为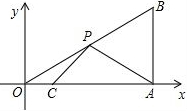 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为 如图,AC=BD,BC:AD=5:9,M是BD的中点.
如图,AC=BD,BC:AD=5:9,M是BD的中点.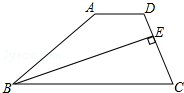 如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )