题目内容
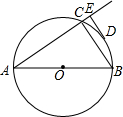 如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是( )
如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是( )①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为弧AD的中点.
| A、①②④ | B、①③④ |
| C、①② | D、②③ |
考点:切线的判定
专题:
分析:连接OD,交BC于点F,可证明DE∥BC,可判断①;在△OCF中,由垂径定理结合勾股定理可求得圆的半径,可判断②;由垂径定理可求得BC的长,结合②可判断③;由弧相等可得弦相等可判断④;可得出答案.
解答: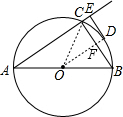 解:如图,连接OD,交BC于点F,连接OC,
解:如图,连接OD,交BC于点F,连接OC,
∵D为弧BC的中点,
∴OD⊥BC,且CF=BF,
又∵AB为⊙O的直径,DE⊥AE,
∴∠BCE=∠DEC=∠CFD=90°,
∴四边形CEDF为矩形,
∴OD⊥DE,
∴DE为⊙O的切线,
故①正确;
∴DF=CE=2cm,CF=DE=6cm,
∴BC=2CF=12cm,
设半径为rcm,则OF=(r-2)cm,
在Rt△OCF中,由勾股定理可得OC2=OF2+CF2,即r2=(r-2)2+62,解得r=10cm,
∴AB=20cm,
故②正确;
在Rt△ABC中,BC=12cm,AB=20cm,
∴AC=
=
=16(cm),
故③不正确;
若C为弧AD的中点,则AC=CD,
在Rt△CDE中,CE=2cm,DE=6cm,由勾股定理可求得CD=2
cm≠AC,
故④不正确;
综上可知正确的为①②,
故选C.
 解:如图,连接OD,交BC于点F,连接OC,
解:如图,连接OD,交BC于点F,连接OC,∵D为弧BC的中点,
∴OD⊥BC,且CF=BF,
又∵AB为⊙O的直径,DE⊥AE,
∴∠BCE=∠DEC=∠CFD=90°,
∴四边形CEDF为矩形,
∴OD⊥DE,
∴DE为⊙O的切线,
故①正确;
∴DF=CE=2cm,CF=DE=6cm,
∴BC=2CF=12cm,
设半径为rcm,则OF=(r-2)cm,
在Rt△OCF中,由勾股定理可得OC2=OF2+CF2,即r2=(r-2)2+62,解得r=10cm,
∴AB=20cm,
故②正确;
在Rt△ABC中,BC=12cm,AB=20cm,
∴AC=
| AB2-BC2 |
| 202-122 |
故③不正确;
若C为弧AD的中点,则AC=CD,
在Rt△CDE中,CE=2cm,DE=6cm,由勾股定理可求得CD=2
| 10 |
故④不正确;
综上可知正确的为①②,
故选C.
点评:本题主要考查切线的判定、垂径定理等知识的综合应用,从D为弧BC的中点为突破口,结合垂径定理、勾股定理求得半径是解题的关键.

练习册系列答案
相关题目
 如图,∠1=15°12′,OA⊥OC,点B、O、D在同一直线上,则∠2的度数为( )
如图,∠1=15°12′,OA⊥OC,点B、O、D在同一直线上,则∠2的度数为( )| A、105.12° |
| B、105.2° |
| C、74.8° |
| D、164.8° |
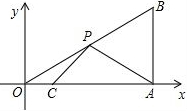 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为 如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.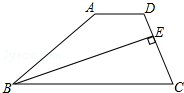 如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( ) 如图,点O在∠APB的平分线上,圆O与PA相切于点C.
如图,点O在∠APB的平分线上,圆O与PA相切于点C. 作图题:已知平面上点A,B,C,D.按下列要求画出图形:
作图题:已知平面上点A,B,C,D.按下列要求画出图形: 已知
已知