题目内容
4. 如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=15°.
如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=15°.
分析 根据常用的三角板的特点求出∠EAD和∠BFD的度数,根据三角形的外角的性质计算即可.
解答 解:由一副常用的三角板的特点可知,∠EAD=45°,∠BFD=30°,
∴∠ABF=∠EAD-∠BFD=15°,
故答案为:15°.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
相关题目
12.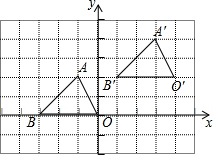 如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
 如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )
如图,△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A′的坐标为(3,4),△ABO内仼意点P(a,b)平移后的对应点P′的坐标为( )| A. | (a,b) | B. | (-a,-b) | C. | (a+2,b+4) | D. | (a+4,b+2) |
9.函数y=$\sqrt{x-2}$+1中,自变量x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
14.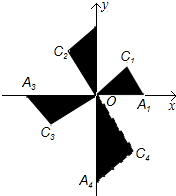 在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
 在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )| A. | 3×($\frac{3}{2}$$\sqrt{3}$)2013 | B. | 3×($\frac{3}{2}\sqrt{3}$)2014 | C. | 3×($\frac{3\sqrt{3}}{2}$)2015 | D. | 3×($\frac{3\sqrt{3}}{2}$)2016 |
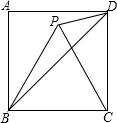 如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP=30°.
如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP=30°.