题目内容
13.若一个扇形的半径为3cm,圆心角为60°,现将此扇形围成一个圆锥的侧面,则这个圆锥的底面积为$\frac{1}{4}$πcm2.分析 易得圆锥的侧面弧长,那么根据圆锥侧面展开图的弧长=底面周长得到圆锥底面半径,进而可求得圆锥的底面积.
解答 解:圆锥的侧面展开是扇形,母线是扇形的半径,则扇形弧长=$\frac{nπr}{180}$=πcm.
那么圆锥的底面半径为:π÷2π=$\frac{1}{2}$,
这个圆锥的底面积为=$\frac{1}{4}$πcm2.
故答案为:$\frac{1}{4}$π.
点评 考查了圆锥的计算,解题的关键是了解圆锥的有关的计算公式,难度不大.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.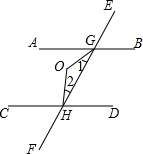 如图,直线AB∥CD,EF分别与AB、CD交于G、H,若∠1=$\frac{1}{3}∠AGH,∠2=\frac{1}{3}$∠CHG,则∠GOH的度数为( )
如图,直线AB∥CD,EF分别与AB、CD交于G、H,若∠1=$\frac{1}{3}∠AGH,∠2=\frac{1}{3}$∠CHG,则∠GOH的度数为( )
 如图,直线AB∥CD,EF分别与AB、CD交于G、H,若∠1=$\frac{1}{3}∠AGH,∠2=\frac{1}{3}$∠CHG,则∠GOH的度数为( )
如图,直线AB∥CD,EF分别与AB、CD交于G、H,若∠1=$\frac{1}{3}∠AGH,∠2=\frac{1}{3}$∠CHG,则∠GOH的度数为( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
5. 将直尺和直角三角板按如图方式摆放,已知∠2=66°,则∠1的大小是( )
将直尺和直角三角板按如图方式摆放,已知∠2=66°,则∠1的大小是( )
 将直尺和直角三角板按如图方式摆放,已知∠2=66°,则∠1的大小是( )
将直尺和直角三角板按如图方式摆放,已知∠2=66°,则∠1的大小是( )| A. | 24° | B. | 34° | C. | 44° | D. | 66° |
3.$\sqrt{2}$的整数部分是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=15°.
如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=15°.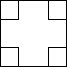
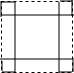

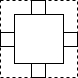
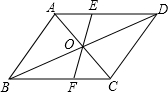 如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=4,BC=6,OE=2,那么四边形EFCD周长是( )
如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=4,BC=6,OE=2,那么四边形EFCD周长是( )