题目内容
16.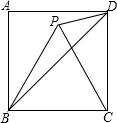 如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP=30°.
如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP=30°.
分析 根据等边三角形的性质和正方形的性质得出BC=DC=CP,∠DCB=90°,∠PCB=60°,求出∠DCP=30°,∠CDB=∠CBD=45°,∠CDP=∠CP=75°,即可求出答案.
解答 解:∵四边形ABCD为正方形,△BPC为等边三角形,
∴BC=DC=CP,∠DCB=90°,∠PCB=60°,
∴∠DCP=90°-60°=30°,∠CDB=∠CBD=45°,
∠CDP=∠CPD=$\frac{1}{2}$(180°-30°)=75°,
∴∠BDP=∠CDP-∠CDB=75°-45°=30°,
故答案为:30°.
点评 本题考查了等边三角形的性质,等腰三角形的性质,正方形的性质的应用,能求出∠CDB和∠CDP的度数是解此题的关键,注意:等边三角形的三边都相等.

练习册系列答案
相关题目
5. 将直尺和直角三角板按如图方式摆放,已知∠2=66°,则∠1的大小是( )
将直尺和直角三角板按如图方式摆放,已知∠2=66°,则∠1的大小是( )
 将直尺和直角三角板按如图方式摆放,已知∠2=66°,则∠1的大小是( )
将直尺和直角三角板按如图方式摆放,已知∠2=66°,则∠1的大小是( )| A. | 24° | B. | 34° | C. | 44° | D. | 66° |
 如图,已知△ABC中,∠C=90°.
如图,已知△ABC中,∠C=90°.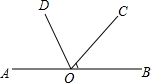 如图,点O在直线AB上,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.
如图,点O在直线AB上,∠BOC=40°,OD平分∠AOC,求∠BOD的度数. 如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=15°.
如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=15°.