题目内容
19.计算:①($\sqrt{5}$+2)($\sqrt{5}$-2)+($\frac{1}{2}$)-2-$\sqrt{25}$
②$\sqrt{12}(\sqrt{75}+3\sqrt{\frac{1}{3}}-\sqrt{48})$.
分析 (1)利用平分差公式和负整数指数幂的意义计算;
(2)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算.
解答 解:(1)原式=5-4+4-5
=0;
(2)原式=2$\sqrt{3}$(5$\sqrt{3}$+$\sqrt{3}$-4$\sqrt{3}$)
=2$\sqrt{3}$×2$\sqrt{3}$
=12.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了负整数指数幂.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
14.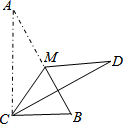 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
9.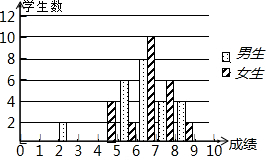 为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?
 为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下(1)请补充完成下面的成绩统计分析表:
| 平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
| 男生 | 6.9 | 2.4 | 7 | 91.7% | 16.7% |
| 女生 | 7 | 1.3 | 7 | 83.3% | 8.3% |
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?
 已知△ABC,求作:AC边上的高.
已知△ABC,求作:AC边上的高.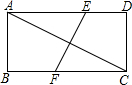 如图,矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E,交BC于点F,则DE=$\frac{3}{2}$.
如图,矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E,交BC于点F,则DE=$\frac{3}{2}$.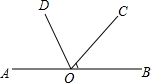 如图,点O在直线AB上,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.
如图,点O在直线AB上,∠BOC=40°,OD平分∠AOC,求∠BOD的度数. 如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=15°.
如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=15°.