��Ŀ����
19����ͼ1����֪������y=-$\frac{1}{2}$x2+bx+c��x��ֱ���A��B���㣬��y�ύ�ڵ�C��A������Ϊ��-2��0����B������Ϊ��4��0����ֱ��l��B��C���㣮��P���߶�BC�ϵ�һ�����㣨��P����B��C�����غϣ����ڵ�P�˶������У�ʼ����һ������P�Һ�y��ƽ�е�ֱ��Ҳ��֮�˶�����ֱ���������ߵĽ���ΪM����x��Ľ���ΪN����1������������ߵĺ�������ʽ����ֱ��д��ֱ��l�ĺ�������ʽ��
��2����ֱ��MN�ѡ�OBC������ֳ�1��3�������֣������ʱ��P�����꣮
��3����ͼ2��������BM��CM�����MBC�������S���ڵ�P���˶������У�S�Ƿ�������ֵ�������ڣ������������ֵ���������ڣ���˵�����ɣ�
�ڵ���MBC��������ʱ��ֱ��MN������һ����E��������ƽ�����Ƿ���ڵ�F��ʹ�Ե�A��P��E��FΪ������ı���Ϊ���Σ������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
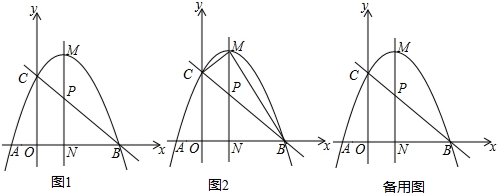
���� ��1���ô���ϵ�����з����������ߺ�ֱ�߽���ʽ���ɣ�
��2���������������ε�����ȵ������Ʊȵ�ƽ�����з�����⣬������������ۣ�
��3�����г�S��x�ĺ�����ϵʽ�����������ֵ���ɣ�
�ڸ������ε����ʺ��ж��������ۣ��з�����⼴�ɣ�
��� �⣺��1���١�A������Ϊ��-2��0����B������Ϊ��4��0����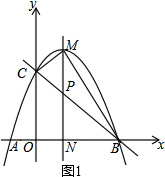
��$\left\{\begin{array}{l}{-2-2b+c=0}\\{-8+4b+c=0}\end{array}\right.$
��ã�b=1��c=4
��y=-$\frac{1}{2}$x2+x+4��
��y=-$\frac{1}{2}$x2+x+4��y��Ľ���C�������ǣ�0��4����B������Ϊ��4��0��
��ֱ��BC�Ľ���ʽΪ��y=-x+4��
��2����ֱ��MN�ѡ�OBC������ֳ�1��3�������֣�MN��y�ᣬ
���BOC�ס�BNP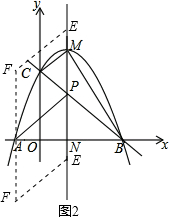
��$\frac{S��BNP}{S��BOC}=\frac{1}{4}$��$\frac{S��BNP}{S��BOC}=\frac{3}{4}$��
��$\frac{PN}{OC}=\frac{1}{2}��\frac{\sqrt{3}}{2}$
��0C=4��
��PN=2��2$\sqrt{3}$
��y=2��2$\sqrt{3}$������y=-x+4�ã�x=2��4-2$\sqrt{3}$��
��P��2��2����P��4-2$\sqrt{3}$��2$\sqrt{3}$����
��3������ͼ1��ʾ���������⣬OC=4��ON=x��BN=4-x��MN=-$\frac{1}{2}$x2+x+4��
��S=S����ONMC+S��BMN-S��BOC
=$\frac{1}{2}��4-\frac{1}{2}{x}^{2}+x+4��•x$+$\frac{1}{2}$����4-x������-$\frac{1}{2}$x2+x+4��-$\frac{1}{2}$��4��4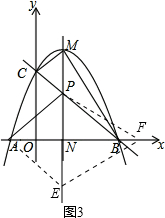
=-x2+4x
=-��x-2��2+4��
�൱x=2ʱ��S�����ֵΪ4��
�ڵ�x=2ʱ��P��2��2������A��-2��0����
��AN=4��PN=2��
��AP=$\sqrt{A{N}^{2}+P{N}^{2}}$=2$\sqrt{5}$��
�Ե�A��P��E��FΪ������ı���Ϊ����ʱ��������4�������
��ͼ2��ʾ��AF��PE��AF=PE=AP=2$\sqrt{5}$��
��F��-2��2$\sqrt{5}$����F��-2��-2$\sqrt{5}$����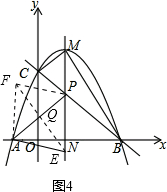
��ͼ3��ʾ���ı���AEFP�����Σ��������ε���Գ��ԣ�FN=4��
OF=ON+FN=2+4=6��
��F��6��0����
��ͼ4��ʾ��EF��ֱƽ��AP��AF=PE=AE��AF��PE��
��NE=m����PE=2+m��AE2=AN2+NE2=42+m2
�ࣨ2+m��2=42+m2
��ã�m=3��
��AF=PE=5��
��F��-2��5����
�����������Ե�A��P��E��FΪ������ı���Ϊ����ʱ����F������Ϊ����-2��2$\sqrt{5}$����F��-2��-2$\sqrt{5}$����F��6��0����F��-2��5����
���� ���⿼���˶��κ����ۺ��ԣ��漰��֪ʶ���У��������ϵ���ص㣬���εĶԳ��ԣ�����ϵ������ֱ�ߵĽ���ʽ��ƽ���ı��ε��ж������ʣ�����˼��ͷ���˼������ã��ۺ��Խ�ǿ����һ�����Ѷȣ�

| A�� | -2 | B�� | -3 | C�� | -4 | D�� | -5 |
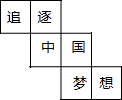 һ���������ƽ��չ��ͼ��ͼ��ʾ��ÿһ���涼��һ�����֣����ڸ��������к͡���������Եĺ����ǣ�������
һ���������ƽ��չ��ͼ��ͼ��ʾ��ÿһ���涼��һ�����֣����ڸ��������к͡���������Եĺ����ǣ�������| A�� | | B�� | �� | C�� | �� | D�� | �� |
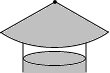 ��ͼ��Ҫ����һ��Բ�ε��̴�ñ��ʹ����Բ�İ뾶��ĸ�߳��ı���4��5����ô����������Ƥ��Բ�Ľ�ӦΪ��������
��ͼ��Ҫ����һ��Բ�ε��̴�ñ��ʹ����Բ�İ뾶��ĸ�߳��ı���4��5����ô����������Ƥ��Բ�Ľ�ӦΪ��������| A�� | 288�� | B�� | 144�� | C�� | 216�� | D�� | 120�� |
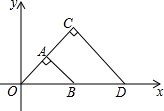 ��ͼ����OAB���OCD���Ե�OΪλ�����ĵ�λ��ͼ�Σ����Ʊ�Ϊ1��2����OCD=90�㣬CO=CD����B��1��0�������C������Ϊ��������
��ͼ����OAB���OCD���Ե�OΪλ�����ĵ�λ��ͼ�Σ����Ʊ�Ϊ1��2����OCD=90�㣬CO=CD����B��1��0�������C������Ϊ��������| A�� | ��1��2�� | B�� | ��1��1�� | C�� | ��$\sqrt{2}$��$\sqrt{2}$�� | D�� | ��2��1�� |
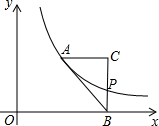 ��֪Rt��ABC����C=90�㣩��һ����״���С���ᷢ���仯��������ֽ�壬��ƽ��ֱ������ϵ�У�����ABC����ͼ���ã�AC��x�ᣬ��B��x���ϣ�����������y=$\frac{4}{x}$��x��0����ͼ����A�����߶�BC�ཻ�ڵ�P����A��P����ĺ�����ֱ�Ϊa��2a+2��
��֪Rt��ABC����C=90�㣩��һ����״���С���ᷢ���仯��������ֽ�壬��ƽ��ֱ������ϵ�У�����ABC����ͼ���ã�AC��x�ᣬ��B��x���ϣ�����������y=$\frac{4}{x}$��x��0����ͼ����A�����߶�BC�ཻ�ڵ�P����A��P����ĺ�����ֱ�Ϊa��2a+2��