题目内容
11.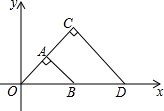 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )| A. | (1,2) | B. | (1,1) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (2,1) |
分析 首先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,ky),进而求出即可.
解答 解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=$\frac{\sqrt{2}}{2}$,
∴A($\frac{1}{2}$,$\frac{1}{2}$),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为:(1,1).
故选:B.
点评 此题主要考查了位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
相关题目
3.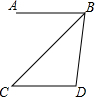 如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )
如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )
 如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )
如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )| A. | 90° | B. | 100° | C. | 110° | D. | 120° |
20.下列调查中,最适宜采用全面调查方式(普查)的是( )
| A. | 对重庆市中学生每天学习所用时间的调查 | |
| B. | 对全国中学生心理健康现状的调查 | |
| C. | 对某班学生进行6月5日是“世界环境日”知晓情况的调查 | |
| D. | 对重庆市初中学生课外阅读量的调查 |
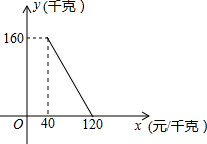 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
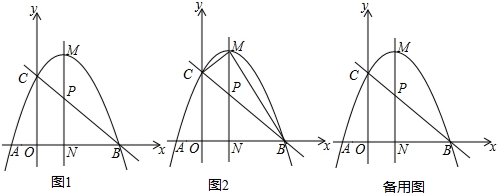
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示. 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴分别相交于点A(-2,0),B(4,0),与y轴交于点C,顶点为点P.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴分别相交于点A(-2,0),B(4,0),与y轴交于点C,顶点为点P.