题目内容
12.已知分式方程$\frac{1}{{x}^{2}-1}$-$\frac{3}{{x}^{2}+x}$=$\frac{2}{{x}^{2}-x}$,求($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)÷$\frac{4-x}{x}$的值.分析 求出分式方程的解得到x的值,原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:分式方程去分母得:x-3(x-1)=2(x+1),
去括号得:x-3x+3=2x+2,
解得:x=$\frac{1}{4}$,
经检验x=$\frac{1}{4}$是分式方程的解,
原式=$\frac{{x}^{2}-4-{x}^{2}+x}{x(x-2)^{2}}$•$\frac{x}{4-x}$=-$\frac{x-4}{x(x-2)^{2}}$•$\frac{x}{x-4}$=-$\frac{1}{(x-2)^{2}}$,
当x=$\frac{1}{4}$时,原式=-$\frac{16}{49}$.
点评 此题考查了分式的化简求值,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.已知方程组$\left\{\begin{array}{l}{3x+5y=k+2}\\{2x+3y=k}\end{array}\right.$的解满足x+y=2,则k的值为( )
| A. | -4 | B. | 2 | C. | -2 | D. | 4 |
1.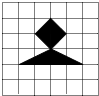 如果小王将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )
如果小王将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )
 如果小王将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )
如果小王将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
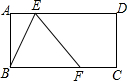 在矩形ABCD中,AB=3,BC=6,将矩形折叠,使B点落在AD(含端点)上,落点记为E,这时折痕与边BC(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF,称为矩形ABCD的“折痕三角形”.当折痕△BEF的面积最大时,AE的长为6-3$\sqrt{3}$.
在矩形ABCD中,AB=3,BC=6,将矩形折叠,使B点落在AD(含端点)上,落点记为E,这时折痕与边BC(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF,称为矩形ABCD的“折痕三角形”.当折痕△BEF的面积最大时,AE的长为6-3$\sqrt{3}$.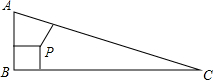 如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离是( )
如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离是( )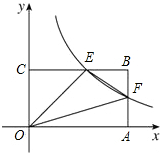 如图,双曲线y=$\frac{4}{x}$(x>0)与矩形OABC的边CB、BA分别交于点E、F,且AF=BF,连接EF,则△OEF的面积为3.
如图,双曲线y=$\frac{4}{x}$(x>0)与矩形OABC的边CB、BA分别交于点E、F,且AF=BF,连接EF,则△OEF的面积为3.