题目内容
13.若-2amb4与5an+2b2m+n可以合并成一项,则mn=1.分析 根据同类项是字母相同且相同字母的指数也相同,可得m、n的值,根据乘方,可得答案.
解答 解:∵-2amb4与5an+2b2m+n可以合并成一项,
∴$\left\{\begin{array}{l}{m=n+2}\\{4=2m+n}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=2}\\{n=0}\end{array}\right.$
∴mn=20=1.
故答案为:1.
点评 本题考查了合并同类项,同类项是字母相同且相同字母的指数也相同是解题关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
1.一家鞋店在一段时间内销售了某种女鞋20双,各种尺码鞋的销售量如表:
(1)求出这些尺码鞋的平均数,中位数,众数.
(2)如果你是老板,去鞋厂进货时哪个尺码的鞋子可以多进一些?为什么?
| 鞋号 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 |
| 人数 | 3 | 4 | 4 | 7 | 1 | 1 |
(2)如果你是老板,去鞋厂进货时哪个尺码的鞋子可以多进一些?为什么?
18.如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.
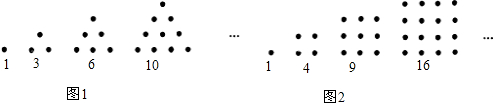
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
(1)按照规律,表格中a=28,b=36,c=35.
(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x-n.
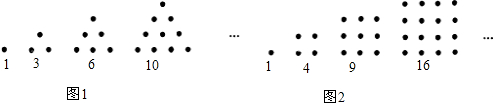
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
| 三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
| 正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
| 五边形数 | 1 | 5 | 12 | 22 | C | 51 | 70 | … |
(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x-n.
5.下列四边形对角线相等但不一定垂直的是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
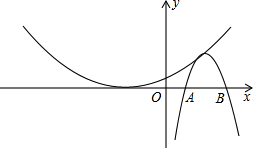 定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.
定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.