题目内容
4.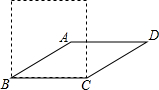 如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.
分析 过A作AM⊥BC于M,求出AM,再根据平行四边形和矩形的面积公式求出即可.
解答 解:如图,过A作AM⊥BC于M,
则∠AMB=90°,
设边长的长度为a,
∵∠B=30°,
∴AM=$\frac{1}{2}$AB=$\frac{1}{2}$a,
∴S2=a×$\frac{1}{2}$a=$\frac{1}{2}$a2,S1=a2,
即S1=2S2,
故答案为:S1=2S2.
点评 本题考查了平行四边形和矩形的性质,含30度角的直角三角形性质的应用,能求出平行四边形和矩形的面积是解此题的关键,难度适中.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
15.下列说法:
(1)在同一平面内,不相交的两条直线一定平行.
(2)在同一平面内,不相交的两条线段一定平行.
(3)相等的角是对顶角.
(4)两条直线被第三条直线所截,同位角相等.
(5)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
其中,正确说法的个数是( )
(1)在同一平面内,不相交的两条直线一定平行.
(2)在同一平面内,不相交的两条线段一定平行.
(3)相等的角是对顶角.
(4)两条直线被第三条直线所截,同位角相等.
(5)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
其中,正确说法的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.下列生活中的现象,属于平移的是( )
| A. | 升降电梯从底楼升到顶楼 | B. | 闹钟的钟摆的运动 | ||
| C. | DVD片在光驱中运行 | D. | 秋天的树叶从树上随风飘落 |




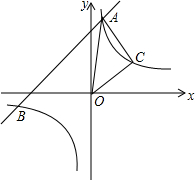 已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2. 小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题: