题目内容
13.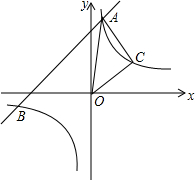 已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2.(1)求m的值;
(2)已知反比例函数在第一象限上有一点C到y轴的距离为3,求△AOC的面积.
分析 (1)根据题意,可得A点的横坐标为x=1,再求出A点坐标为(1,6),将A点坐标代入${y_2}=\frac{m}{x}$,即可求出m的值;
(2)由点C到y轴的距离为3,得出C点的横坐标为3,将x=3代入反比例函数解析式,求出y,得到C点坐标.过A、C分别向x轴作垂线,垂足为E、F,根据反比例函数比例系数k的几何意义得到S△AOE=S△COF=$\frac{1}{2}$×6=3,那么S△AOC=S△AOE+S直角梯形AEFC-S△COF=S直角梯形AEFC=$\frac{1}{2}$(2+6)×(3-1)=8.
解答 解:(1)∵一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2,
∴A点的横坐标为x=1,
将x=1代入y1=x+5中,得y=6,
∴A(1,6),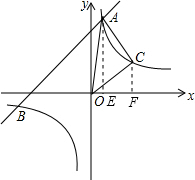 将A(1,6)代入${y_2}=\frac{m}{x}$,得m=1×6=6;
将A(1,6)代入${y_2}=\frac{m}{x}$,得m=1×6=6;
(2)∵点C到y轴的距离为3,
∴C点的横坐标为3,
又C在双曲线上,
∴y=$\frac{6}{3}$,即C(3,2).
过A、C分别向x轴作垂线,垂足为E、F,则S△AOE=S△COF=$\frac{1}{2}$×6=3.
S△AOC=S△AOE+S直角梯形AEFC-S△COF
=S直角梯形AEFC
=$\frac{1}{2}$(2+6)×(3-1)
=8.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了待定系数法求反比例函数的解析式,三角形的面积,反比例函数比例系数k的几何意义.

练习册系列答案
相关题目
5. 某市一周平均气温(℃)如图所示,下列说法不正确的是( )
某市一周平均气温(℃)如图所示,下列说法不正确的是( )
 某市一周平均气温(℃)如图所示,下列说法不正确的是( )
某市一周平均气温(℃)如图所示,下列说法不正确的是( )| A. | 星期二的平均气温最高 | B. | 星期四到星期日天气逐渐转暖 | ||
| C. | 这一周最高气温与最低气温相差4℃ | D. | 星期四的平均气温最低 |
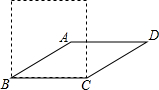 如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,使∠ABC=30°.设矩形面积为s1、平行四边形ABCD面积为s2,则s1与s2的关系为S1=2S2.
 如图,在平行四边形ABCD中,已知M和N分别是边AB、DC的中点,试说明四边形BMDN也是平行四边形.
如图,在平行四边形ABCD中,已知M和N分别是边AB、DC的中点,试说明四边形BMDN也是平行四边形. 如图,已知反比例函数 y1=$\frac{m}{x}$(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,4)与点A,且与反比例函数的图象相交于另一点B.
如图,已知反比例函数 y1=$\frac{m}{x}$(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,4)与点A,且与反比例函数的图象相交于另一点B. 如图,一次函数y=x-2图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(3,m),与x轴交于点B.
如图,一次函数y=x-2图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(3,m),与x轴交于点B.