题目内容
18.某小区共有5000个家庭,为了了解辖区居民的住房情况,居民委员会随机调查了本辖区内一定数量的家庭的住房面积,并将调查的资料绘制成直方图和扇形图.(m~n中含右端点,不含左端点)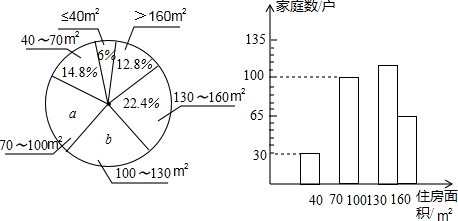
请你根据以上不完整的直方图和扇形图提供的信息,解答下列问题:
(1)这次共调查了多少个家庭的住房面积?扇形图中的a、b的值分别是多少?
(2)补全频数分布直方图;
(3)被调查的家庭中,在未来5年内,计划购买第二套住房的家庭统计如下表:
| 住房面和(m2) | ≤40 | 40~70 | 70~100 | 100~130 | 130~160 | >160 |
| $\frac{计划购第二套房的家庭数}{被调查的家庭数}$ | 0 | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{1}{16}$ | $\frac{1}{32}$ |
分析 (1)由不超过40平方米的家庭数和所占的百分比求出调查的家庭总数,利用频率的求法就求出a=100÷500,b=1-20%-14.8%-6%-12.8%-22.4%;
(2)利用总数和百分比求出缺少的频数,再补全统计图;
(3)根据表格中的数据求得所调查的500户家庭中计划未来5年内买房的家庭数,进而估计出全市的家庭数.
解答 解:(1)这次共调查了500户家庭,扇形图中a=20%,b=24%.
(2)根据题意得:500×14.8%=74,500×24%=120.补全频数分布直方图如下.
(3)所调查的500户家庭中计划未来5年内买房的有:
30×0+74×$\frac{1}{2}$+100×$\frac{1}{4}$+120×$\frac{1}{8}$+500×22.4%×$\frac{1}{16}$+500×12.8%×$\frac{1}{32}$=86(户),
由此可以预测该小区在未来五年计划购买第二套住房的家庭有$\frac{86}{500}$×5000=860个.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
3.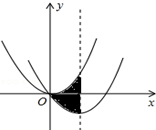 如图,在平面直角坐标系中,抛物线y=$\frac{1}{3}$x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{8}{3}$,则a、b的值分别为( )
如图,在平面直角坐标系中,抛物线y=$\frac{1}{3}$x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{8}{3}$,则a、b的值分别为( )
 如图,在平面直角坐标系中,抛物线y=$\frac{1}{3}$x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{8}{3}$,则a、b的值分别为( )
如图,在平面直角坐标系中,抛物线y=$\frac{1}{3}$x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{8}{3}$,则a、b的值分别为( )| A. | $\frac{1}{3}$,$\frac{4}{3}$ | B. | $\frac{1}{3}$,-$\frac{8}{3}$ | C. | $\frac{1}{3}$,-$\frac{4}{3}$ | D. | -$\frac{1}{3}$,$\frac{4}{3}$ |
10. 如图所示,AB∥CD,NP平分∠MNB,已知∠1=20°,则∠2=( )
如图所示,AB∥CD,NP平分∠MNB,已知∠1=20°,则∠2=( )
 如图所示,AB∥CD,NP平分∠MNB,已知∠1=20°,则∠2=( )
如图所示,AB∥CD,NP平分∠MNB,已知∠1=20°,则∠2=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |

 如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相交于点M.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.
如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相交于点M.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.