��Ŀ����
3��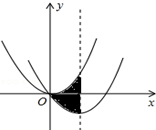 ��ͼ����ƽ��ֱ������ϵ�У�������y=$\frac{1}{3}$x2����ƽ�Ƶõ�������y=ax2+bx����Գ�����������������Χ�ɵ���Ӱ���ֵ����Ϊ$\frac{8}{3}$����a��b��ֵ�ֱ�Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У�������y=$\frac{1}{3}$x2����ƽ�Ƶõ�������y=ax2+bx����Գ�����������������Χ�ɵ���Ӱ���ֵ����Ϊ$\frac{8}{3}$����a��b��ֵ�ֱ�Ϊ��������| A�� | $\frac{1}{3}$��$\frac{4}{3}$ | B�� | $\frac{1}{3}$��-$\frac{8}{3}$ | C�� | $\frac{1}{3}$��-$\frac{4}{3}$ | D�� | -$\frac{1}{3}$��$\frac{4}{3}$ |
���� ȷ����������y=ax2+bx�Ķ������꣬Ȼ����������ߵĶԳ�����ԭ�����ߵĽ������꣬�Ӷ��жϳ���Ӱ���ֵ�������������ε�������ٸ��������ε������ʽ��ʽ���㼴�ɵý⣮
��� �⣺��ͼ ��
��
��y=ax2+bx=$\frac{1}{3}$x2+bx=$\frac{1}{3}$��x+$\frac{3b}{2}$��2-$\frac{3{b}^{2}}{4}$��
��ƽ�ƺ������ߵĶ�������Ϊ��-$\frac{3b}{2}$��-$\frac{3{b}^{2}}{4}$�����Գ���Ϊֱ��x=-$\frac{3b}{2}$��
��x=-$\frac{3b}{2}$ʱ��y=$\frac{3{b}^{2}}{4}$��
��ƽ�ƺ���Ӱ���ֵ����������ͼ�����ε������
$\frac{1}{2}$����$\frac{3{b}^{2}}{4}$+$\frac{3{b}^{2}}{4}$������-$\frac{3b}{2}$��=$\frac{8}{3}$��
���b=-$\frac{4}{3}$��
��ѡ��C��
���� ���⿼���˶��κ���ͼ���뼸�α任��ȷ��������Ӱ���������ȵ��������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
�����Ŀ
14�����м��㣬��ȷ���ǣ�������
| A�� | x3•x4=x12 | B�� | ��3x��3=27x3 | C�� | ��x3��3=x6 | D�� | 2x2��x=x |
18��ijС������5000����ͥ��Ϊ���˽�Ͻ�������ס�����������ίԱ����������˱�Ͻ����һ�������ļ�ͥ��ס�������������������ϻ��Ƴ�ֱ��ͼ������ͼ����m��n�к��Ҷ˵㣬������˵㣩
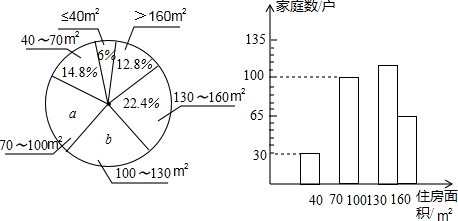
����������ϲ�������ֱ��ͼ������ͼ�ṩ����Ϣ������������⣺
��1����ι������˶��ٸ���ͥ��ס�����������ͼ�е�a��b��ֵ�ֱ��Ƕ��٣�
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��������ļ�ͥ�У���δ��5���ڣ��ƻ�����ڶ���ס���ļ�ͥͳ�����±���
������ε��飬���Ʊ�С����δ����5���ڣ����ж��ٸ���ͥ�ƻ�����ڶ���ס����

����������ϲ�������ֱ��ͼ������ͼ�ṩ����Ϣ������������⣺
��1����ι������˶��ٸ���ͥ��ס�����������ͼ�е�a��b��ֵ�ֱ��Ƕ��٣�
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��������ļ�ͥ�У���δ��5���ڣ��ƻ�����ڶ���ס���ļ�ͥͳ�����±���
| ס����ͣ�m2�� | ��40 | 40��70 | 70��100 | 100��130 | 130��160 | ��160 |
| $\frac{�ƻ����ڶ����ļ�ͥ��}{������ļ�ͥ��}$ | 0 | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{1}{16}$ | $\frac{1}{32}$ |
8�����е����У����ʺ�ʹ���ղ���ǣ�������
| A�� | ��������ij�������Ŀ���ר��2BǦ������ | |
| B�� | ����ȫ����ѧ���ԡ����ܰɣ��ֵܡ���Ŀ��ϲ���̶� | |
| C�� | ����ij��˾������һ��ţ�̵ı����� | |
| D�� | ����ijУ������2����Ů��������μƻ� |
 ��ͼ������ABCD�ǹ�һ��������ͣ�ŵij�λʾ��ͼ����֪BC=2m��CD=5.4m����DCF=30�㣬������㳵λ��ռ�Ŀ���EFԼΪ�����ף��������ȷ��0.1m��$\sqrt{3}$��1.73��
��ͼ������ABCD�ǹ�һ��������ͣ�ŵij�λʾ��ͼ����֪BC=2m��CD=5.4m����DCF=30�㣬������㳵λ��ռ�Ŀ���EFԼΪ�����ף��������ȷ��0.1m��$\sqrt{3}$��1.73��