题目内容
11.现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
分析 根据题意可以通过列表的方法写出所有的可能性,从而可以得到所得结果之和为9的概率.
解答 解:由题意可得,
同时投掷这两枚骰子,所得的所有结果是:
(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6)、
(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6)、
(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6)、
(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6)、
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)、
(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6),
则所有结果之和是:
2、3、4、5、6、7、
3、4、5、6、7、8、
4、5、6、7、8、9、
5、6、7、8、9、10、
6、7、8、9、10、11、
7、8、9、10、11、12,
∴所得结果之和为9的概率是:$\frac{4}{36}=\frac{1}{9}$,
故选C.
点评 本题考查列表法和树状图法,解题的关键是明确题意,列出相应的表格,计算出相应的概率.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
2. 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
6. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
16.-3的绝对值是( )
| A. | $\frac{1}{3}$ | B. | -3 | C. | 3 | D. | ±3 |
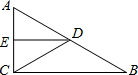 如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12.
如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12. 如图,已知四边形ABCD内接于⊙O,A是$\widehat{BDC}$的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且$\widehat{BF}=\widehat{AD}$.
如图,已知四边形ABCD内接于⊙O,A是$\widehat{BDC}$的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且$\widehat{BF}=\widehat{AD}$.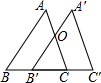 如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为2.5cm.
如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为2.5cm.