题目内容
19. 如图,已知四边形ABCD内接于⊙O,A是$\widehat{BDC}$的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且$\widehat{BF}=\widehat{AD}$.
如图,已知四边形ABCD内接于⊙O,A是$\widehat{BDC}$的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且$\widehat{BF}=\widehat{AD}$.(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
分析 (1)欲证△ADC∽△EBA,只要证明两个角对应相等就可以.可以转化为证明且$\widehat{BF}=\widehat{AD}$就可以;
(2)A是$\widehat{BDC}$的中点,的中点,则AC=AB=8,根据△CAD∽△ABE得到∠CAD=∠AEC,求得AE,根据正切三角函数的定义就可以求出结论.
解答 (1)证明:∵四边形ABCD内接于⊙O,
∴∠CDA=∠ABE.
∵$\widehat{BF}=\widehat{AD}$,
∴∠DCA=∠BAE.
∴△ADC∽△EBA;
(2)解:∵A是$\widehat{BDC}$的中点,
∴$\widehat{AB}=\widehat{AC}$
∴AB=AC=8,
∵△ADC∽△EBA,
∴∠CAD=∠AEC,$\frac{DC}{AB}=\frac{AC}{AE}$,
即$\frac{5}{8}=\frac{8}{AE}$,
∴AE=$\frac{64}{5}$,
∴tan∠CAD=tan∠AEC=$\frac{AC}{AE}$=$\frac{8}{\frac{64}{5}}$=$\frac{5}{8}$.
点评 本题考查的是圆的综合题,涉及到弧、弦的关系,等腰三角形的性质,相似三角形的判定与性质等知识,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
相关题目
7.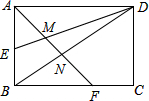 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )| A. | $\frac{2\sqrt{2}}{5}$ | B. | $\frac{9\sqrt{2}}{20}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{4\sqrt{2}}{5}$ |
14.为了让书籍开拓学生的视野,陶冶学生的情操,向阳中学开展了“五个一”课外阅读活动,为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
(1)将表中空格处的数据补全,完成上面的频数、频率分布表;
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
| 组别 | 分组 | 频数(人数) | 频率 |
| 1 | 10≤t<30 | 0.16 | |
| 2 | 30≤t<50 | 20 | |
| 3 | 50≤t<70 | 0.28 | |
| 4 | 70≤t<90 | 6 | |
| 5 | 90≤t<110 |
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
11.现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
8.已知圆锥的底面半径为4cm,母线长为6cm,则它的侧面展开图的面积等于( )
| A. | 24cm2 | B. | 48cm2 | C. | 24πcm2 | D. | 12πcm2 |




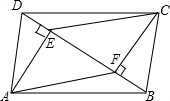 四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.
四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.