题目内容
1．某村种的水稻前年平均每公顷产7 200kg，今年平均每公顷产8 450kg．设这两年该村水稻每公顷产量的年平均增长率为x，根据题意，所列方程为7200（1+x）2=8450．分析 由题意得：第一年水稻产量7200（1+x），第二年水稻产量：7200（1+x）（1+x），进而可得方程7200（1+x）2=8450．
解答 解：设这两年该村水稻每公顷产量的年平均增长率为x，根据题意得：
7200（1+x）2=8450，
故答案为：7200（1+x）2=8450．
点评 此题主要考查了由实际问题抽象出一元二次方程，关键是掌握求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．
练习册系列答案
相关题目
11．计算3a2÷$\frac{1}{3}$a4=（ ）
| A． | 9a6 | B． | a6 | C． | $\frac{9}{{a}^{-2}}$ | D． | $\frac{9}{{a}^{2}}$ |
如图，直线AB、CD相交于O，MO⊥AB于O，∠BOC：∠BON=4：1，OM平分∠NOC．求∠MON、∠BOD的度数．
9．
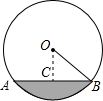一条排水管的截面如下左图所示，已知排水管的半径OB=10，水面宽AB=16，则排水管内水的最大深度是（ ）
一条排水管的截面如下左图所示，已知排水管的半径OB=10，水面宽AB=16，则排水管内水的最大深度是（ ）| A． | 4 | B． | 5 | C． | 6$\sqrt{3}$ | D． | 6 |
13．
如图，某轮船在O处，测得灯塔A在它北偏东40°的方向上，渔船B在它的东南方向上，则∠AOB的度数是（ ）
如图，某轮船在O处，测得灯塔A在它北偏东40°的方向上，渔船B在它的东南方向上，则∠AOB的度数是（ ）| A． | 85° | B． | 90° | C． | 95° | D． | 100° |
如图，平行四边形ABCD中，E、F分别为AB、AD上的点，且BE=2AE，AF=3DF，连结EF、AC，交于点G，则$\frac{AG}{CG}$的值为$\frac{3}{10}$．