题目内容
1. 如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )| A. | 12π | B. | 24π | C. | 6π | D. | 36π |
分析 根据题意得出AB=AB′=12,∠BAB′=60°,根据图形得出图中阴影部分的面积S=$\frac{60π×{12}^{2}}{360}$+$\frac{1}{2}$π×62-$\frac{1}{2}$π×62,求出即可.
解答 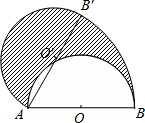 解:∵AB=AB′=12,∠BAB′=60°
解:∵AB=AB′=12,∠BAB′=60°
∴图中阴影部分的面积是:
S=S扇形B′AB+S半圆O′-S半圆O
=$\frac{60π×{12}^{2}}{360}$+$\frac{1}{2}$π×62-$\frac{1}{2}$π×62
=24π.
故选B.
点评 本题考查的是扇形的面积及旋转的性质,通过做此题培养了学生的计算能力和观察图形的能力,题目比较好,难度适中.

练习册系列答案
相关题目
12. 如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
 如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )| A. | 圆形铁片的半径是4cm | B. | 四边形AOBC为正方形 | ||
| C. | 弧AB的长度为4πcm | D. | 扇形OAB的面积是4πcm2 |
 已知:如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE.
已知:如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE.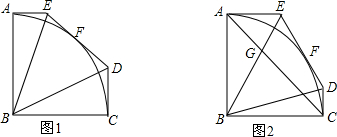
 兴的实际距离约为80km.
兴的实际距离约为80km.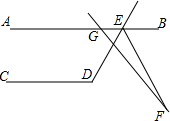 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F=9.5°.
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F=9.5°.