题目内容
16.五边形ABCDE中,∠EAB=∠ABC=∠BCD=90°,AB=BC,且满足以点B为圆心,AB长为半径的圆弧AC与边DE相切于点F,连接BE,BD.(1)如图1,求∠EBD的度数;
(2)如图2,连接AC,分别与BE,BD相交于点G,H,若AB=1,∠DBC=15°,求AG•HC的值.
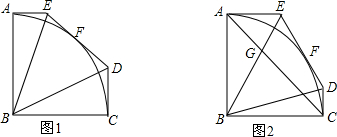
分析 (1)如图1,连接BF,由DE与⊙B相切于点F,得到BF⊥DE,通过Rt△BAE≌Rt△BFE,得到∠1=∠2,同理∠3=∠4,于是结论可得;
(2)如图2,连接BF并延长交CD的延长线于P,由△ABE≌△CBP,得到PB=BE=$\frac{2\sqrt{3}}{3}$,求出PF=$\frac{2\sqrt{3}}{3}-1$,通过△AEG∽△CHD,列比例式即可得到结果.
解答 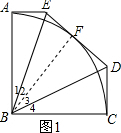 解:(1)如图1,连接BF,
解:(1)如图1,连接BF,
∵DE与⊙B相切于点F,
∴BF⊥DE,
在Rt△BAE与Rt△BFE中,$\left\{\begin{array}{l}{BA=BF}\\{BE=BE}\end{array}\right.$,
∴Rt△BAE≌Rt△BFE,
∴∠1=∠2,
同理∠3=∠4,
∵∠ABC=90°,
∴∠2+∠3=45°,
即∠EBD=45°;
(2)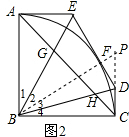 如图2,连接BF并延长交CD的延长线于P,
如图2,连接BF并延长交CD的延长线于P,
∵∠4=15°,
由(1)知,∠3=∠4=15°,
∴∠1=∠2=30°,∠CBP=30°,
∵∠EAB=∠PCB=90°,AB=1,
∴AE=$\frac{\sqrt{3}}{3}$,BE=$\frac{2\sqrt{3}}{3}$,
在△ABE与△CBP中,$\left\{\begin{array}{l}{∠1=∠CBP}\\{AB=BC}\\{∠BAE=∠BCP}\end{array}\right.$,
∴△ABE≌△CBP,
∴PB=BE=$\frac{2\sqrt{3}}{3}$,
∴PF=$\frac{2\sqrt{3}}{3}-1$,
∵∠P=60°,
∴DF=2-$\sqrt{3}$,
∴CD=DF=2-$\sqrt{3}$,
∵∠EAG=∠DCH=45°,
∠AGE=∠BDC=75°,
∴△AEG∽△CHD,
∴$\frac{AG}{CD}=\frac{AE}{CH}$,
∴AG•CH=CD•AE,
∴AG•CH=CD•AE=(2-$\sqrt{3}$)•$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}-3}{3}$.
点评 本题考查了切线的性质,全等三角形的判定和性质,相似三角形的判定和性质,画出辅助线构造全等三角形是解题的关键.

 阅读快车系列答案
阅读快车系列答案 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )| A. | AB=BE | B. | BE⊥DC | C. | ∠ADB=90° | D. | CE⊥DE |
 如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )| A. | 12π | B. | 24π | C. | 6π | D. | 36π |
| A. |  | B. |  | C. |  | D. |  |
| 年龄(单位:岁) | 12 | 13 | 14 | 15 |
| 人数 | 3 | 5 | 6 | 4 |
| A. | 13岁,14岁 | B. | 14岁,14岁 | C. | 14岁,13岁 | D. | 14岁,15岁 |
 如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.



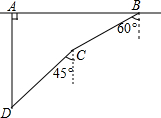 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).