题目内容
12. 如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )| A. | 圆形铁片的半径是4cm | B. | 四边形AOBC为正方形 | ||
| C. | 弧AB的长度为4πcm | D. | 扇形OAB的面积是4πcm2 |
分析 由BC,AC分别是⊙O的切线,B,A为切点,得到OA⊥CA,OB⊥BC,又∠C=90°,OA=OB,推出四边形AOBC是正方形,得到OA=AC=4,故A,B正确;根据扇形的弧长、面积的计算公式求出结果即可进行判断.
解答 解:由题意得:BC,AC分别是⊙O的切线,B,A为切点,
∴OA⊥CA,OB⊥BC,
又∵∠C=90°,OA=OB,
∴四边形AOBC是正方形,
∴OA=AC=4,故A,B正确;
∴$\widehat{AB}$的长度为:$\frac{90•4π}{180}$=2π,故C错误;
S扇形OAB=$\frac{90•{π4}^{2}}{360}$=4π,故D正确.
故选C.
点评 本题考查了切线的性质,正方形的判定和性质,扇形的弧长、面积的计算,熟记计算公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
 如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )| A. | 12π | B. | 24π | C. | 6π | D. | 36π |
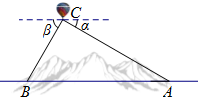 2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数)
2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数) 如图,点P、Q是反比例函数y=$\frac{k}{x}$图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1,△QMN的面积记为S2,则S1=S2.(填“>”或“<”或“=”)
如图,点P、Q是反比例函数y=$\frac{k}{x}$图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1,△QMN的面积记为S2,则S1=S2.(填“>”或“<”或“=”) 如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省2元.
如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省2元.



 实数a,b在数轴上的位置如图所示,则$\sqrt{{a}^{2}}$-|a-b|=-b.
实数a,b在数轴上的位置如图所示,则$\sqrt{{a}^{2}}$-|a-b|=-b.