题目内容
7.在△ABC中,∠C=90°,根据下列条件解直角三角形:(1)∠B=60°,a=3$\sqrt{3}$
(2)c=10,∠B=45°
(3)a=3$\sqrt{2}$,b=3$\sqrt{6}$
(4)∠A=2∠B,c-b=8.
分析 (1)先利用互余计算出∠A,再利用正切的定义求出b,利用含30度对的边等于斜边的一半得到c的值;
(2)先利用互余计算出∠A,再利用勾股定理求得a,b;
(3)先利用勾股定理计算出c,再利用正切的定义求出∠A,然后利用互余计算∠B;
(4)先利用∠A=2∠B,∠A+∠B=90°求得∠A,∠B,再利用含30度对的边等于斜边的一半得到得到方程,即可得到结果.
解答 解:(1)∵∠B=60°,
∴∠A=30°,
∵tanA=$\frac{a}{b}$=$\frac{\sqrt{3}}{3}$,
∴b=9,c=2a=6$\sqrt{3}$;
(2)∵∠B=45°,
∴∠A=45°,
∴a=b=csinA=5$\sqrt{2}$;
(3)由勾股定理得:c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{(3\sqrt{2})^{2}+(3\sqrt{6})^{2}}$=6$\sqrt{2}$,
∵tanA=$\frac{a}{b}$=$\frac{3\sqrt{2}}{3\sqrt{6}}$=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
∴∠B=90°-∠A=60°;
(4)∵∠A=2∠B,∠A+∠B=90°,
∴∠A=60°,∠B=30°,
∴c=2b,
∵c-b=8,
∴b=8,c=16,
∴a=$\sqrt{{c}^{2}-{b}^{2}}$=8$\sqrt{3}$.
点评 本题主要考查三角函数的定义,掌握解直角三角形的方法步骤是解题的关键,即有角先求角,有斜用弦,有直有切.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
17.方程x2-3x-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
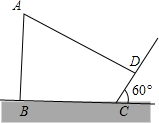 小刚在利用阳光下的影子测量大树AB的高度时,大树的影子恰好落在了山坡坡面CD和地面BC上,他用2m长的竹竿测得CD=4m,BC=10m,用量角器测得斜坡CD与地面BC成60°角,如图所示,且测得此时长2m的竹竿的影长为1m,求大树AB的高度.(结果可保留根号)
小刚在利用阳光下的影子测量大树AB的高度时,大树的影子恰好落在了山坡坡面CD和地面BC上,他用2m长的竹竿测得CD=4m,BC=10m,用量角器测得斜坡CD与地面BC成60°角,如图所示,且测得此时长2m的竹竿的影长为1m,求大树AB的高度.(结果可保留根号) 如图,△ABC中,∠1=∠2,∠ABC=∠C,∠1=∠C,求∠4的度数.
如图,△ABC中,∠1=∠2,∠ABC=∠C,∠1=∠C,求∠4的度数.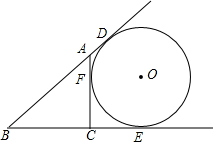 如图所示,已知AC⊥BC,BC=4,AC=3,⊙O与直线AB,BC,CA都相切,切点分别为D,E,F.求⊙O的半径.
如图所示,已知AC⊥BC,BC=4,AC=3,⊙O与直线AB,BC,CA都相切,切点分别为D,E,F.求⊙O的半径.