Question

15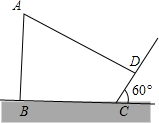．小刚在利用阳光下的影子测量大树AB的高度时，大树的影子恰好落在了山坡坡面CD和地面BC上，他用2m长的竹竿测得CD=4m，BC=10m，用量角器测得斜坡CD与地面BC成60°角，如图所示，且测得此时长2m的竹竿的影长为1m，求大树AB的高度．（结果可保留根号）

Answer 1

分析 根据题意利用锐角三角函数关系得出EC，DE的长，再利用长2m的竹竿的影长为1m，进而得出EF的长，进而得出AB的长．

解答 解：过点D作DE⊥BC延长线于点E，延长AD交BC延长线于点F，
∵DC=4m，∠DCE=60°，
∴EC=2m，DE=2$\sqrt{3}$m，
∵测得此时长2m的竹竿的影长为1m，
∴EF=$\sqrt{3}$m，
∵BC+EC+EF=10+2+$\sqrt{3}$=（12+$\sqrt{3}$）m，
∴大树AB的高度为：2（12+$\sqrt{3}$）=（24+2$\sqrt{3}$）m．

点评 此题主要考查了解直角三角形的应用以及坡度与坡角问题，求出AB的长影长是解题关键．