题目内容
15．
如图，梯形ABCD中，AD∥BC，AC交BD于点O．若S△AOD=4，S△AOB=6，则△COD的面积是6．
分析 直接利用梯形的性质得出S△ABD=S△ADC，进而得出△COD的面积．
解答 解：∵梯形ABCD中，AD∥BC，AD=AD，
∴S△ABD=S△ADC，
∴S△AOB=S△DOC，
∵S△AOD=4，S△AOB=6，
∴△COD的面积是6．
故答案为：6．
点评 此题主要考查了梯形，正确得出S△ABD=S△ADC是解题关键．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
5．1-4个月的婴儿生长发育非常快，他们的体重y（g）与月龄x（月）间的关系如表所示．
请写出y与x之间的关系式y=700x+3500．
请写出y与x之间的关系式y=700x+3500．
| 月龄/月 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 体重/g | 3500 | 4200 | 4900 | 5600 | 6300 | 7000 | 7700 |
如图，△ABC中，高BD、CE相交于点H，若∠A：∠ABC：∠ACB=3：2：4，则∠BHC=120°．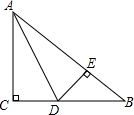
如图，在△ABC中，∠C=90°，AC=BC，AD平分∠CAB，交BC于D，DE⊥AB于E，且△ACD的周长为30，AD=13cm，则斜边AB长为17cm．
20．下列各对数中，互为相反数的是（ ）
| A． | +（-2）和-（+2） | B． | -|-3|和+（-3） | C． | （-1）2和-12 | D． | （-1）3和-13 |
