题目内容
10.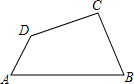 如图,在四边形ABCD的边AB上任取一点O(不与点A、B重合)连接OC、OD,分别取OA、OB、OC、OD的中点A′、B′、C′、D′,连接A′D′、D′C′、C′B′、,四边形A′B′C′D′与四边形ABCD相似吗?为什么?
如图,在四边形ABCD的边AB上任取一点O(不与点A、B重合)连接OC、OD,分别取OA、OB、OC、OD的中点A′、B′、C′、D′,连接A′D′、D′C′、C′B′、,四边形A′B′C′D′与四边形ABCD相似吗?为什么?
分析 根据三角形的中位线定理证明两个多边形对应边的比相等、对应角相等即可得到答案.
解答 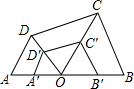 解:四边形A′B′C′D′∽四边形ABCD,
解:四边形A′B′C′D′∽四边形ABCD,
证明:∵A′、D′是OA、OD的中点,
∴A′D′∥AD,A′D′=$\frac{1}{2}$AD,
∴$\frac{A′D′}{AD}$=$\frac{1}{2}$,
同理$\frac{C′D′}{CD}$=$\frac{B′C′}{BC}$$\frac{A′B′}{AB}$=$\frac{1}{2}$,
∵A′D′∥AD,
∴∠OA′D′=∠OAD,∠OD′A′=∠ODA,
可以证明:两个四边形的对应角相等,
∴四边形A′B′C′D′∽四边形ABCD.
点评 本题考查的是相似多边形的性质、三角形中位线定理,掌握相似多边形的判定定理、灵活运用三角形中位线定理是解题的关键.

练习册系列答案
相关题目
1.下列运算中,正确的是( )
| A. | 5a2b-5ba2=0 | B. | 3a+2b=5ab | C. | 2x3+3x3=5x6 | D. | 5y2-4y2=1 |
2.已知实数a、b、c满足a>0,a+c<b,则一定有( )
| A. | b2-4ac≥0 | B. | b2-4ac>0 | C. | b2-4ac≤0 | D. | b2-4ac<0 |
20.几个小朋友分一堆糖,若每人k颗,还剩14颗,若每人(k+1)颗,最后一个人只分到6颗,计算小朋友人数及k的值分别是( )
| A. | 17人,k=8 | B. | 17人,k=9 | C. | 11人,k=10 | D. | 11人,k=8 |
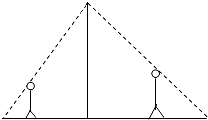 如图,小明和他的父亲晚饭后到广场去散步,休息时小明站在广场中电灯的左侧,距离电灯支杆的距离为3米,影长为1米,小明的父亲站在电灯的右侧,他距离电灯支杆的距离为4.3米.已知小明的身高为1.5米,小明父亲身高为1.7米,则此时小明父亲的影长为多少米?
如图,小明和他的父亲晚饭后到广场去散步,休息时小明站在广场中电灯的左侧,距离电灯支杆的距离为3米,影长为1米,小明的父亲站在电灯的右侧,他距离电灯支杆的距离为4.3米.已知小明的身高为1.5米,小明父亲身高为1.7米,则此时小明父亲的影长为多少米? 如图,在圆内接四边形ABCD中,DC=DB,M为CA延长线上一点.
如图,在圆内接四边形ABCD中,DC=DB,M为CA延长线上一点.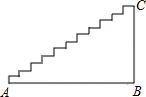 某宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红地毯,如果主楼梯的坡度为1:$\sqrt{3}$,且楼梯的竖直高度为3m.至少需要多长的地毯?(精确到0.1m)
某宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红地毯,如果主楼梯的坡度为1:$\sqrt{3}$,且楼梯的竖直高度为3m.至少需要多长的地毯?(精确到0.1m)