题目内容
5. 如图,在圆内接四边形ABCD中,DC=DB,M为CA延长线上一点.
如图,在圆内接四边形ABCD中,DC=DB,M为CA延长线上一点.求证:AD平分∠BAM.
分析 根据圆内接四边形的性质得到∠MAD=∠DBC,根据等腰三角形的性质得到∠DBC=∠DCB,根据圆周角定理得到∠DAB=∠DCB,证明结论.
解答 证明:∵四边形ABCD是圆内接四边形,
∴∠MAD=∠DBC,
∠DAB=∠DCB,
∵DC=DB,
∴∠DBC=∠DCB,
∴∠MAD=∠DAB,
即AD平分∠BAM.
点评 本题考查的是圆内接四边形的性质以及等腰三角形的性质,掌握圆内接四边形的外角等于它的内对角是解题的关键.

练习册系列答案
相关题目
16.化简-(+4)的结果是( )
| A. | -4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | 4 |
17.下表是中超联赛中A,B,C,D,E五支球队的积分及胜负情况
(1)从B队积分可以看出,平一场积1分;
(2)从C队积分可以看出,负一场积0分;
(3)再从A队积分可以看出,胜一场积3分;
(4)观察D,E队提供的信息,可得a=14,b=6,c=8.
| 队名 | 比赛场次 | 胜场 | 平场 | 负场 | 积分 |
| A | 16 | 8 | 4 | 4 | 28 |
| B | 16 | 0 | 16 | 0 | 16 |
| C | 16 | 0 | 12 | 4 | 12 |
| D | 16 | 2 | 8 | 3 | a |
| E | 16 | b | c | 2 | 26 |
(2)从C队积分可以看出,负一场积0分;
(3)再从A队积分可以看出,胜一场积3分;
(4)观察D,E队提供的信息,可得a=14,b=6,c=8.
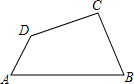 如图,在四边形ABCD的边AB上任取一点O(不与点A、B重合)连接OC、OD,分别取OA、OB、OC、OD的中点A′、B′、C′、D′,连接A′D′、D′C′、C′B′、,四边形A′B′C′D′与四边形ABCD相似吗?为什么?
如图,在四边形ABCD的边AB上任取一点O(不与点A、B重合)连接OC、OD,分别取OA、OB、OC、OD的中点A′、B′、C′、D′,连接A′D′、D′C′、C′B′、,四边形A′B′C′D′与四边形ABCD相似吗?为什么?