题目内容
已知两条直线y1=-ax+b和y2=-bx+a,其中a<0,b>0,它们在同一直角坐标系中的图象可能是( )
A、 |
B、 |
C、 |
D、 |
考点:一次函数图象与系数的关系
专题:
分析:因为a<0,b>0,所以-a>0,-b<0,可以判断直线y1=-ax+b经过一、二、三、象限,直线y2=-bx+a经过二、三、四象限,即可判定.
解答:解:∵a<0,b>0,
∴-a>0,-b<0,
∴y1随x的增大而增大,且交y轴的正半轴,y2随x的增大而减小,且交y轴的负半轴,
所以直线y1=-ax+b经过一、二、三、象限,直线y2=-bx+a经过二、三、四象限,
故选D.
∴-a>0,-b<0,
∴y1随x的增大而增大,且交y轴的正半轴,y2随x的增大而减小,且交y轴的负半轴,
所以直线y1=-ax+b经过一、二、三、象限,直线y2=-bx+a经过二、三、四象限,
故选D.
点评:此题主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限.
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
数轴上的点a,b对应的数是0,+1的相反数,点c对应的数是x,点c与点a的距离大于点c与点b的距离,则( )
| A、x>0 | ||
| B、x>-1 | ||
C、x<-
| ||
| D、x<-1 |
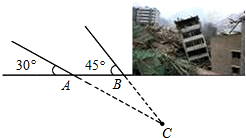 某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3m,探测线与地面的夹角分别是35°和45°,试确定生命所在点C的深度.(参考数据:
某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3m,探测线与地面的夹角分别是35°和45°,试确定生命所在点C的深度.(参考数据: