题目内容
5．
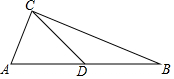如图，△ABC中，AC=5，BC=12，AB=13，CD是AB边上的中线．则CD=6.5．
分析 先根据勾股定理的逆定理判定△ABC为直角三角形，然后根据直角三角形的性质即可得到结论．
解答 解：∵在△ABC中，AC=5，BC=12，AB=13，
∴AC2+BC2=52+122=132=AB2，
∴△ABC为直角三角形，且∠ACB=90°，
∵CD是AB边上的中线，
∴CD=6.5；
故答案为：6.5．
点评 本题考查了勾股定理的逆定理和直角三角形的性质的综合应用．先判定△ABC为直角三角形是解题的关键．
练习册系列答案
相关题目
15．下列函数是二次函数的有（ ）
（1）y=1-x2；（2）y=$\frac{2}{{x}^{2}}$；（3）y=x（x-3）；（4）y=ax2+bx+c；（5）y=2x+1；（6）y=2（x+3）2-2x2．
（1）y=1-x2；（2）y=$\frac{2}{{x}^{2}}$；（3）y=x（x-3）；（4）y=ax2+bx+c；（5）y=2x+1；（6）y=2（x+3）2-2x2．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．
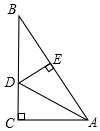如图，在Rt△ABC中，∠C=90°，AD平分∠CAB，点D到AB的距离DE=1cm，BE=$\sqrt{3}$cm，则BC等于（ ）
如图，在Rt△ABC中，∠C=90°，AD平分∠CAB，点D到AB的距离DE=1cm，BE=$\sqrt{3}$cm，则BC等于（ ）| A． | 1cm | B． | 2cm | C． | 3cm | D． | （$\sqrt{3}$+1）cm |
10．“服务他人，提升自我”，某学校积极开展志愿者服务活动，来自初三的5名同学（3男3女）成立了“交通秩序维护”小分队，若从该小分队中任选两名同学进行交通秩序维护，则恰好是一男一女的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |
17．
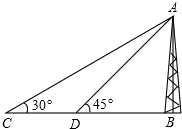如图，在塔AB前的平地上选择一点C，测出看塔顶的仰角为30°，从C点向塔底走100米到达D点，测出看塔顶的仰角为45°，则塔AB的高为（ ）
如图，在塔AB前的平地上选择一点C，测出看塔顶的仰角为30°，从C点向塔底走100米到达D点，测出看塔顶的仰角为45°，则塔AB的高为（ ）| A． | 50$\sqrt{3}$米 | B． | 100$\sqrt{3}$米 | C． | 50（$\sqrt{3}$+1）米 | D． | 50（$\sqrt{3}$-1）米 |
14．函数y=$\sqrt{x-1}$+2中，自变量x的取值范围是（ ）
| A． | x≥1 | B． | x＞1 | C． | x＜1 | D． | x≤1 |
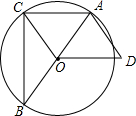如图，已知△ABC内接于⊙O，AB是直径，OD∥AC，AD=OC．