题目内容
已知?ABCD的周长为26,∠ABC=120°,BD为一条对角线,⊙O内切于△ABD,E,F,G为切点,已知⊙O的半径为
.求?ABCD的面积.
| 3 |
考点:三角形的内切圆与内心,全等三角形的判定与性质,平行四边形的性质
专题:
分析:首先运用三边及⊙O的半径表示出平行四边形的面积;根据题意求出AB+AD=13;借助切线的性质求出BD的长度问题即可解决.
解答:解:设⊙O分别切△ABD的边AD、AB、BD于点G、E、F;
平行四边形ABCD的面积为S;
则S=2S△ABD=2×
(AB•OE+BD•OF+AD•OG),
=
(AB+AD+BD);
∵平行四边形ABCD的周长为26,
∴AB+AD=13,
∴S=
(13+BD);连接OA;
由题意得:∠OAE=30°,
∴AG=AE=3;同理可证DF=DG,BF=BE;
∴DF+BF=DG+BE=13-3-3=7,
即BD=7,
∴S=
(13+7)=20
.
即平行四边形ABCD的面积为20
.
平行四边形ABCD的面积为S;
则S=2S△ABD=2×
| 1 |
| 2 |
=
| 3 |
∵平行四边形ABCD的周长为26,
∴AB+AD=13,
∴S=
| 3 |
由题意得:∠OAE=30°,
∴AG=AE=3;同理可证DF=DG,BF=BE;
∴DF+BF=DG+BE=13-3-3=7,
即BD=7,
∴S=
| 3 |
| 3 |
即平行四边形ABCD的面积为20
| 3 |
点评:该题考查了三角形内切圆的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
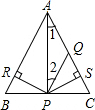 如图,△ABC中,∠1=∠2,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AB;③△BRP≌△QSP,( )
如图,△ABC中,∠1=∠2,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AB;③△BRP≌△QSP,( )| A、全部正确 | B、①和②正确 |
| C、仅①正确 | D、①和③正确 |
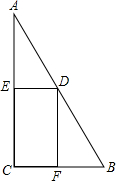 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )| A、逐渐减小 |
| B、逐渐增大 |
| C、先增大后减小 |
| D、先减小后增大 |
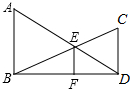 已知,如图所示,AB∥CD,AD交BC于点E,EF∥AB交BD于点F.
已知,如图所示,AB∥CD,AD交BC于点E,EF∥AB交BD于点F. 已知点A和直线m,用尺规作图作出点A关于直线m的轴对称点.
已知点A和直线m,用尺规作图作出点A关于直线m的轴对称点.