题目内容
利用二次函数的图象求抛物线y=x2-6x+1与直线y=-2x+4交点坐标的近似值?
考点:图象法求一元二次方程的近似根
专题:
分析:在同一平面直角坐标系中画出抛物线y=x2-6x+1与直线y=-2x+4,它们交点坐标的近似值即为所求.
解答:解:作出二次函数y=x2-6x+1的图象与直线y=-2x+4,如图所示,

由图象可知,抛物线y=x2-6x+1与直线y=-2x+4交点坐标的近似值为(-0.65,5.30),(4.65,-5.30).

由图象可知,抛物线y=x2-6x+1与直线y=-2x+4交点坐标的近似值为(-0.65,5.30),(4.65,-5.30).
点评:本题考查了图象法求两函数交点坐标的近似根,准确画出函数的图象是解题的关键.

练习册系列答案
相关题目
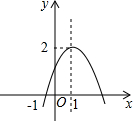 如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:
如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:①abc<0;②x=1时,函数的最大值是2;③a+2b+4c<0;④2a=-b;⑤2c>3b.其中
正确的结论有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
如果(x-2)(x+3)=x2+px-q,那么p、q的值是( )
| A、p=1,q=-6 |
| B、p=5,q=6 |
| C、p=1,q=6 |
| D、p=5,q=-6 |
 射线OA,BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s,t分别表示行驶距离和时间,则下列说法错误的是( )
射线OA,BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s,t分别表示行驶距离和时间,则下列说法错误的是( )| A、当t=4小时时,乙在甲的前面 |
| B、当t=5小时时,甲追上乙 |
| C、甲、乙两人同时同地出发 |
| D、甲的速度比乙的速度更大 |
若△ABC∽△A′B′C′,其面积比为1:2,则△ABC与△A′B′C′的相似比为( )
| A、1:2 | ||
B、
| ||
| C、1:4 | ||
D、
|
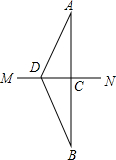 如图,A、B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?
如图,A、B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么? 某轮船由西向东航行,在A处测得小岛P的方位是北偏东70°,又继续航行7海里后,在B处测得小岛P的方位是北偏东50°,则此时轮船与小岛P的距离BP=
某轮船由西向东航行,在A处测得小岛P的方位是北偏东70°,又继续航行7海里后,在B处测得小岛P的方位是北偏东50°,则此时轮船与小岛P的距离BP=