题目内容
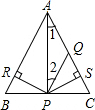 如图,△ABC中,∠1=∠2,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AB;③△BRP≌△QSP,( )
如图,△ABC中,∠1=∠2,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AB;③△BRP≌△QSP,( )| A、全部正确 | B、①和②正确 |
| C、仅①正确 | D、①和③正确 |
考点:全等三角形的判定与性质
专题:
分析:易证RT△APR≌RT△APS,可得AS=AR,∠BAP=∠1,再根据∠1=∠2即可求得QP∥AB,即可解题.
解答:解:∵在RT△APR和RT△APS中,
,
∴RT△APR≌RT△APS,(HL)
∴∠AR=AS,①正确,
∠BAP=∠1,
∵∠1=∠2,
∴∠BAP=∠2,
∴QP∥AB,②正确,
∵△BRP和△QSP中,只有一个条件PR=PS,再没有其余条件可以证明△BRP≌△QSP,故③错误;
故选 B.
|
∴RT△APR≌RT△APS,(HL)
∴∠AR=AS,①正确,
∠BAP=∠1,
∵∠1=∠2,
∴∠BAP=∠2,
∴QP∥AB,②正确,
∵△BRP和△QSP中,只有一个条件PR=PS,再没有其余条件可以证明△BRP≌△QSP,故③错误;
故选 B.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证RT△APR≌RT△APS是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
在数轴上与点-2的距离为4的点所表示的数是( )
| A、-6 | B、2 | C、±3 | D、-6或2 |
 已知四边形ABCD的面积为4,∠ADC=∠B=90°,AD=DC,求点D到AB的距离DF.
已知四边形ABCD的面积为4,∠ADC=∠B=90°,AD=DC,求点D到AB的距离DF.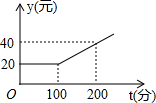 已知甲、乙两家通信公司都推出了市话通话优惠业务,甲公司每月的市话费标准如图所示,乙公司每月通话收费标准如表所示.
已知甲、乙两家通信公司都推出了市话通话优惠业务,甲公司每月的市话费标准如图所示,乙公司每月通话收费标准如表所示. 如图所示,直线AB、CD相交于点O,OE是∠AOD的平分线,∠FOC=90°,∠1=70°,求∠2与∠3的度数.
如图所示,直线AB、CD相交于点O,OE是∠AOD的平分线,∠FOC=90°,∠1=70°,求∠2与∠3的度数.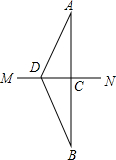 如图,A、B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?
如图,A、B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?