题目内容
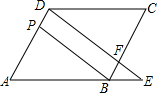 如图,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出并写出三组不同的相似三角形:
如图,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出并写出三组不同的相似三角形:考点:相似三角形的判定,平行四边形的性质
专题:
分析:可利用平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似判断即可.
解答:解:∵BP∥DF,
∴△ABP∽△AED;
∴四边形ABCD是平行四边形,
∴DC∥AB,BC∥AD,
∴△CDF∽△BEF,△EFB∽△EDA,
故答案为:△ABP∽△AED,△CDF∽△BEF,△EFB∽△EDA.
∴△ABP∽△AED;
∴四边形ABCD是平行四边形,
∴DC∥AB,BC∥AD,
∴△CDF∽△BEF,△EFB∽△EDA,
故答案为:△ABP∽△AED,△CDF∽△BEF,△EFB∽△EDA.
点评:本题考查了相似三角形的判定与性质:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.

练习册系列答案
相关题目
请你运用学过的函数知识,判断下列哪一个图象可能是函数y=x3的图象( )
A、 |
B、 |
C、 |
D、 |
 如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠MOC=35°20′,则∠BON的度数为( )
如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠MOC=35°20′,则∠BON的度数为( )| A、35°20′ |
| B、45°20′ |
| C、54°40′ |
| D、64°40′ |
从下列物体抽象出来的几何体可以看成圆柱的是( )
A、 |
B、 |
C、 |
D、 |
 如图将两块三角板的直角顶点重叠在一起,∠DOB与∠DOA的比是2:11,则∠BOC=
如图将两块三角板的直角顶点重叠在一起,∠DOB与∠DOA的比是2:11,则∠BOC= 已知
已知
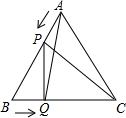 如图,P、Q是边长为6cm的等边△ABC边AB、BC上两动点,点P从点A,点Q从点B同时出发,运动时间为t秒,速度是1cm/s,则当△BPQ是直角三角形时,t的值是
如图,P、Q是边长为6cm的等边△ABC边AB、BC上两动点,点P从点A,点Q从点B同时出发,运动时间为t秒,速度是1cm/s,则当△BPQ是直角三角形时,t的值是 如图,AB∥EF,∠CDE=∠E,求证:AB∥CD.
如图,AB∥EF,∠CDE=∠E,求证:AB∥CD.