题目内容
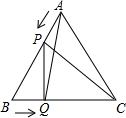 如图,P、Q是边长为6cm的等边△ABC边AB、BC上两动点,点P从点A,点Q从点B同时出发,运动时间为t秒,速度是1cm/s,则当△BPQ是直角三角形时,t的值是
如图,P、Q是边长为6cm的等边△ABC边AB、BC上两动点,点P从点A,点Q从点B同时出发,运动时间为t秒,速度是1cm/s,则当△BPQ是直角三角形时,t的值是考点:等边三角形的性质
专题:动点型,分类讨论
分析:分两种情况考虑:(i)当PQ⊥BC时,如图所示,由速度是1厘米/秒,时间是t秒,利用速度×时间=路程表示出AP与BQ的长,再由AB-AP表示BP,由三角形ABC为等边三角形,得到∠B=60°,在直角三角形BPQ中,利用锐角三角函数定义及特殊角的三角函数值列出关于t的方程,求出方程的解即可得到t的值;(ii)当QP⊥AB时,如图所示,由速度是1厘米/秒,时间是t秒,利用速度×时间=路程表示出AP与BQ的长,再由AB-AP表示BP,由三角形ABC为等边三角形,得到∠B=60°,在直角三角形BPQ中,利用锐角三角函数定义及特殊角的三角函数值列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.
解答: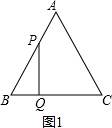 解:分两种情况考虑:
解:分两种情况考虑:
(i)当PQ⊥BC时,如图1所示:
由题意可得:AP=BQ=tcm,BP=(6-t)cm,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=
=
,即
=
,
解得:t=2秒;
(ii)当QP⊥AB时,如图2所示: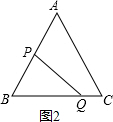
由题意可得:AP=BQ=tcm,BP=(6-t)cm,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=
=
,即
=
,
解得:t=4秒,
综上所述,t的值是2秒或4秒.
故答案为:2秒或4秒.
 解:分两种情况考虑:
解:分两种情况考虑:(i)当PQ⊥BC时,如图1所示:
由题意可得:AP=BQ=tcm,BP=(6-t)cm,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=
| BQ |
| BP |
| 1 |
| 2 |
| t |
| 6-t |
| 1 |
| 2 |
解得:t=2秒;
(ii)当QP⊥AB时,如图2所示:

由题意可得:AP=BQ=tcm,BP=(6-t)cm,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=
| BP |
| BQ |
| 1 |
| 2 |
| 6-t |
| t |
| 1 |
| 2 |
解得:t=4秒,
综上所述,t的值是2秒或4秒.
故答案为:2秒或4秒.
点评:此题考查了等边三角形的性质,锐角三角函数定义,特殊角的三角函数值,利用了分类讨论及方程的思想,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
下列说法:①若-1<b<0,则b>
;②若∠AOP=∠BOP,则OP平分∠AOB;③同旁内角互补,那么它们的两条角平分线互相垂直;④两条直线相交有且只有一个交点,其中正确的个数是( )
| 1 |
| b |
| A、1个 | B、2个 | C、3个 | D、4个 |
在Rt△ABC中,把各边都缩小到
,那么sinA的值( )
| 1 |
| 5 |
A、都缩小
| ||
| B、都不变 | ||
| C、都扩大5倍 | ||
| D、无法确定 |
 如图,直线AD与CE相交于点O,若∠COB=44°,∠AOB=90°.则∠AOE等于( )
如图,直线AD与CE相交于点O,若∠COB=44°,∠AOB=90°.则∠AOE等于( )| A、56° | B、44° |
| C、45° | D、46° |
下列各式中,正确的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.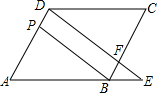 如图,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出并写出三组不同的相似三角形:
如图,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出并写出三组不同的相似三角形:
 如图,在△ABD和△ACD中,∠1=∠2,请你再补充一个条件,使△ABD≌△ACD,补充的条件是
如图,在△ABD和△ACD中,∠1=∠2,请你再补充一个条件,使△ABD≌△ACD,补充的条件是