题目内容
 如图,AB∥EF,∠CDE=∠E,求证:AB∥CD.
如图,AB∥EF,∠CDE=∠E,求证:AB∥CD.考点:平行线的判定与性质
专题:证明题
分析:由AB∥EF可得到∠B=∠E,结合条件可得∠B=∠CDE,由同位角相等,两直线平行,可判定AB∥CD.
解答:证明:
∵AB∥EF,
∴∠B=∠E,
又∠CDE=∠E,
∴∠CDE=∠B,
∴AB∥CD.
∵AB∥EF,
∴∠B=∠E,
又∠CDE=∠E,
∴∠CDE=∠B,
∴AB∥CD.
点评:本题主要考查平行线的判定和性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列式子从左到右变形中,是因式分解的为( )
| A、a2+4a•21=a(a+4)•21 |
| B、a2+4a-21=(a-3)(a+7) |
| C、(a-3)(a+7)=a2+4a-21 |
| D、a2+4a-21=(a+2)2-25 |
下列各式中,正确的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
已知x2-2x-3=0,则4x-2x2的值为( )
| A、-6 | B、6 |
| C、-2或6 | D、-2或30 |
化简
÷
的结果是( )
| m-1 |
| m |
| 1-m |
| m2 |
| A、m | ||
B、
| ||
| C、-m | ||
D、-
|
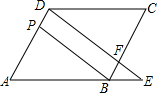 如图,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出并写出三组不同的相似三角形:
如图,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出并写出三组不同的相似三角形: 如图,在△ABD和△ACD中,∠1=∠2,请你再补充一个条件,使△ABD≌△ACD,补充的条件是
如图,在△ABD和△ACD中,∠1=∠2,请你再补充一个条件,使△ABD≌△ACD,补充的条件是