题目内容
12.观察下列各等式:$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…,根据你发现的规律计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$=$\frac{2016}{2017}$.分析 根据等式的变化找出变化规律“$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$”,依此规律将原式展开即可得出结论.
解答 解:∵$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…,
∴$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$.
故答案为:$\frac{2016}{2017}$.
点评 本题考查了规律型中数字的变化类,根据等式的变化找出变化规律“$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$”是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.若菱形的周长为52cm,面积为120cm2,则它的对角线之和为( )
| A. | 14cm | B. | 17cm | C. | 28cm | D. | 34cm |
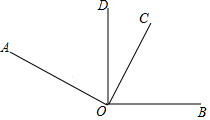 如图,已知∠AOB=155°,∠AOC=∠BOD=90°.
如图,已知∠AOB=155°,∠AOC=∠BOD=90°.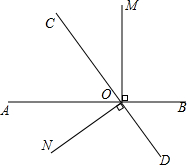 如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.