题目内容
4.如图,二次函数y=kx2-3kx-4k(k≠0),的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,OC=OA.(1)求点A坐标和抛物线的解析式;
(2)是否存在抛物线上的点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过抛物线上的点Q作垂直于y轴的直线,交y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,直接写出点Q的坐标.
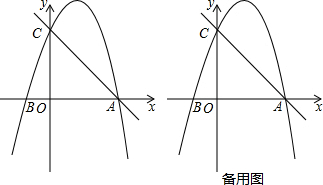
分析 (1)只需令y=0就可求出点A、B的坐标,由OC=OA可得到点C的坐标,然后把点C的坐标代入抛物线的解析式就可解决问题;
(2)只需分∠ACP=90°或∠CAP=90°两种情况讨论,就可求出点P的坐标;
(3)易证四边形OEDF是矩形,则有EF=OD.要使EF最短,只需OD最短,只需OD⊥AC,由此可求出DF即yQ,然后只需把yQ代入抛物线的解析式就可解决问题.
解答 解:(1)当y=0时,kx2-3kx-4k=0
∵k≠0,∴x2-3x-4=0,
解得:x1=-1,x2=4
∴B(-1,0),A(4,0),
∵OA=OC,
∴C(0,4);
把x=0,y=4代入y=kx2-3kx-4k,
得k=-1,
则抛物线的解析式为:y=-x2+3x+4;
(2)①当∠PCA=90°时,过点P作PM⊥y轴于M,如图1,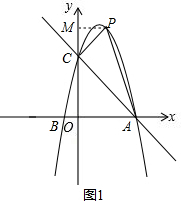
∴∠MCP+∠ACO=90°.
∵∠OAC+∠ACO=90°,
∴∠MCP=∠OAC.
∵OA=OC,
∴∠MCP=∠OAC=45°,
∴∠MCP=∠MPC=45°,
∴MC=MP.
设P(m,-m2+3m+4),
则PM=CM=m,OM=-m2+3m+4,
∴m+4=-m2+3m+4,
解得:m1=0(舍去),m2=2,
∴-m2+3m+4=6,
即P(2,6);
②当∠PAC=90°时,过点P作PN⊥y轴于N,设AP与y轴交于点F,如图2,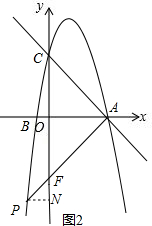
则有PN∥x轴,
∴∠FPN=∠OAP.
∵∠CAO=45°,∴∠OAP=45°,
∴∠FPN=45°,AO=OF=4,
∴PN=NF,
设P(n,-n2+3n+4),
则PN=-n,ON=n2-3n-4,
∴-n+4=n2-3n-4,
解得:n1=-2,n2=4(舍去),
∴-n2+3n+4=-6,
即P(-2,-6).
综上所述:点P的坐标是(2,6)或(-2,-6);
(3)当点Q的坐标是($\frac{3+\sqrt{17}}{2}$,2)或($\frac{3-\sqrt{17}}{2}$,2)时,EF最短.
提示:如图3,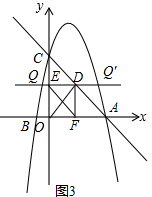
∵∠OED=∠DFO=∠EOF=90°,
∴四边形OEDF是矩形,
∴EF=OD.
∴当线段EF的长度最短时,OD最小,
此时OD⊥AC.
∵OA=OC,
∴∠COD=∠AOD=45°,CD=AD.
∵DF∥OC,∴△ADF∽△ACO,
∴$\frac{DF}{OC}$=$\frac{AD}{AC}$=$\frac{1}{2}$,
∴DF=$\frac{1}{2}$OC=2,
∴yQ=2,
解-x2+3x+4=2,得
x1=$\frac{3+\sqrt{17}}{2}$,x2=$\frac{3-\sqrt{17}}{2}$,
∴点Q的坐标是($\frac{3+\sqrt{17}}{2}$,2)或($\frac{3-\sqrt{17}}{2}$,2).
点评 本题主要考查了抛物线上点的特征、解直角三角形、解一元二次方程、相似三角形的判定与性质、矩形的判定与性质、勾股定理等知识,运用分类讨论的思想是解决第(2)小题的关键,利用矩形的对角线相等将EF转化为OD,是解决第(3)小题的关键.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | (a+4)(a-4)=a2-4 | B. | 2a2-3a=-a | C. | a6÷a3=a2 | D. | (a2)3=a6 |
| A. | m-2>n+2 | B. | 2m>2n | C. | -$\frac{m}{2}$>$\frac{n}{2}$ | D. | m2>n2 |
 如图,有3张不透明的卡片,除正面写有不同的数字外,其他均相同,将这3张卡片背面向上洗匀,从中随机抽取一张,记下数字后放回;重新洗匀后再从中随机抽取一张,将抽取的第一张、第二张卡片上的数字分别作为十位数字和个位数字组成两位数,请用画树状图(或列表)的方法,求这个两位数能被3整除的概率.
如图,有3张不透明的卡片,除正面写有不同的数字外,其他均相同,将这3张卡片背面向上洗匀,从中随机抽取一张,记下数字后放回;重新洗匀后再从中随机抽取一张,将抽取的第一张、第二张卡片上的数字分别作为十位数字和个位数字组成两位数,请用画树状图(或列表)的方法,求这个两位数能被3整除的概率.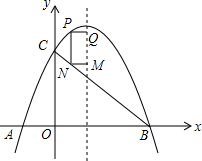 如图,平面直角坐标系中,抛物线y=ax2+bx+2与x轴分别交于点A(-1,0)、B(3,0),与y轴交于点C,连结BC.点P是BC上方抛物线上一点,过点P作y轴的平行线,交BC于点N,分别过P、N两点作x轴的平行线,交抛物线的对称轴于点Q、M,设P点的横坐标为m.
如图,平面直角坐标系中,抛物线y=ax2+bx+2与x轴分别交于点A(-1,0)、B(3,0),与y轴交于点C,连结BC.点P是BC上方抛物线上一点,过点P作y轴的平行线,交BC于点N,分别过P、N两点作x轴的平行线,交抛物线的对称轴于点Q、M,设P点的横坐标为m.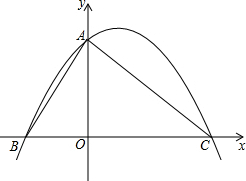 将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).
将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).