题目内容
14.我们已经学习了一元二次方程的三种解法:因式分解法,配方法和公式法.请选择你认为适当的方法解下列方程.①x2-3x+1=0;
②(x+4)2=5(x+4);
③x2-2x=4.
分析 ①方程利用公式法求出解即可;
②方程利用因式分解法求出解即可;
③方程利用配方法求出解即可.
解答 解:①△=(-3)2-4×1×1=5,
∴x=$\frac{3±\sqrt{5}}{2}$,
解得:x1=$\frac{3+\sqrt{5}}{2}$,x2=$\frac{3-\sqrt{5}}{2}$;
②方程移项得:(x+4)2-5(x+4)=0,
分解因式得:(x+4)(x+4-5)=0,
解得:x1=-4,x2=1;
③配方得:x2-2x+1=4+1,即(x-1)2=5,
开方得:x-1=±$\sqrt{5}$,
解得:x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$.
点评 此题考查了解一元二次方程-因式分解法,配方法,以及公式法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
4.把二次函数y=x2的图象向右平移2个单位,再向下平移5个单位,所得图象对应的函数式是( )
| A. | y=(x-2)2-5 | B. | y=(x-2)2+5 | C. | y=(x+2)2-5 | D. | y=(x+2)2-5 |
5.下列计算正确的是( )
| A. | 8x9÷4x3=2x3 | B. | k7+k7=2k14 | ||
| C. | a8•a8=2a16 | D. | 2ab2c÷(-$\frac{1}{2}$)ab2=-4c |
2.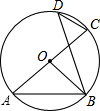 如图,AC是⊙O的直径,点B,D在⊙O上,那么图中等于∠BOC一半的角有( )
如图,AC是⊙O的直径,点B,D在⊙O上,那么图中等于∠BOC一半的角有( )
 如图,AC是⊙O的直径,点B,D在⊙O上,那么图中等于∠BOC一半的角有( )
如图,AC是⊙O的直径,点B,D在⊙O上,那么图中等于∠BOC一半的角有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | l个 |
4.下列计算正确的是( )
| A. | (-a)5÷(-a)2=-a3 | B. | x6÷x2=x6÷2=x3 | C. | (-a)7÷a5=a2 | D. | (-x)8÷(-x)6=-x2 |
