题目内容
2．
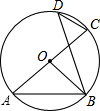如图，AC是⊙O的直径，点B，D在⊙O上，那么图中等于∠BOC一半的角有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | l个 |
分析 根据圆周角定理可得∠CDB=$\frac{1}{2}$∠BOC，∠CAB=$\frac{1}{2}$∠BOC，再根据等边对等角可得∠OBA=∠OAB，进而可得∠OBA=$\frac{1}{2}$∠BOC．
解答 解：∠CDB=$\frac{1}{2}$∠BOC，∠CAB=$\frac{1}{2}$∠BOC，
∵AO=BO，
∴∠OBA=∠OAB，
∴∠OBA=$\frac{1}{2}$∠BOC，
共3个，
故选：B．
点评 此题主要考查了圆周角定理，关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
12．若$\sqrt{a+b+5}$+|2a-b+1|=0，则（b-a）2005的值为（ ）
| A． | -1 | B． | 1 | C． | 52005 | D． | -52005 |
17．若$\frac{x}{y}$=$\frac{3}{4}$，则$\frac{x+y}{y}$的值为（ ）
| A． | 1 | B． | $\frac{4}{7}$ | C． | $\frac{5}{4}$ | D． | $\frac{7}{4}$ |
7．要组织一次篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排21场比赛．设参赛球队的个数为x，则根据题意所列的方程是（ ）
| A． | x2=21 | B． | $\frac{1}{2}$x（x+1）=21 | C． | $\frac{1}{2}{x}^{2}$=21 | D． | x（x-1）=21 |
12．下列式子成立的是（ ）
| A． | $\sqrt{（-2）^{2}}$=-2 | B． | （-$\sqrt{3}$）2=9 | C． | $\sqrt{9}$=±3 | D． | $\root{3}{-8}$=-2 |