题目内容

对于形如x2+2xa+a2这样的二次三项式，可以用公式法将它分解成（x+a）2的形式．但对于二次三项式x2+2xa+3a2，就不能直接运用公式了．小红是这样想的：在二次三项式x2+2xa-3a2中先加上一项a2，使它与x2+2xa的和成为一个完全平方式，再减去a2，整个式子的值不变，于是有：
x2+2xa-3a2=（x2+2xa+a2）-a2-3a2
=（x+a）2-4a2
=（x+a）2-（2a）2
=（x+3a）（x-a）
像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”．
参考小红思考问题的方法，利用“配方法”把a2-6a+8进行因式分解．
考点：配方法的应用
专题：阅读型
分析：要运用配方法，只要二次项系数为1，只需加上一次项系数一半的平方即可配成完全平方公式．
解答：解：a2-6a+8
=a2-6a+9-1
=（a-3）2-1
=（a-2）（a-4）．
点评：此题考查了配方法的应用．配方法：先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变．
练习册系列答案
相关题目
如果不等式组
x+8＜4x-1
x＞m
的解集是x＞4，那么m的取值范围是（　　）
A、m≥4B、m≤4
C、m=4D、m＜4
如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：
①AD∥BC；
②∠ACB=2∠ADB；
③∠ADC=90°-∠ABD；
④BD平分∠ADC；
⑤∠BDC=
1
2
∠BAC．
其中正确的结论有（　　）
A、2个B、3个C、4个D、5个
某校八年级学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：
1号2号3号4号5号总数
甲班891009611897500
乙班1009511091104500
经统计发现两班总数相等．此时有学生建议，可以通过考察数据中的其他信息作为参考．请你回答下列问题：
（1）计算两班的优秀率．
（2）求两班比赛成绩的中位数．
（3）估计两班比赛数据的方差哪一个小？
（4）根据以上三条信息，你认为应该把冠军奖状发给哪一个班级？简述你的由．
如图，已知：点B、E、F、C在同一直线上，∠A=∠D，BE=CF，且AB∥CD．求证：AF∥ED
证明：∵BE=FC
∴BE+EF=FC+EF（
 
）
即：
 

∵AB∥CD
∴∠B=∠C（
 
）
∠A=∠D
∠B=∠C
在△ABF和△DCE中，有
BF=CE
∴△ABF≌△DCE（
 
）
∴∠AFB=∠DEC（
 
）
∴AF∥ED（
 
）
已知：在正方形ABCD中，E、G分别是射线CB、DA上的两个动点，点F是CD边上，满足EG⊥BF，

（1）如图1，当E、G在CB、DA边上运动时（不与正方形顶点重合），求证：GE=BF．
（2）如图2，在（1）的情况下，连结GF，求证：FG+BE＞
2
BF．
（3）如图3，当E、G运动到BC、AD的反向延长线时，请你直接写出FG、BE、BF三者的数量关系（不必写出证明过程）．
在一次知识竞赛中，甲、乙两人进入了“必答题”环节．规则是：两人轮流答题，每人都要回答20个题，每个题回答正确得m分，回答错误或放弃回答扣n分．当甲、乙两人恰好都答完12个题时，甲答对了9个题，得分为39分；乙答对了10个题，得分为46分．
（1）求m和n的值；
（2）规定此环节得分不低于60分能晋级，甲在剩下的比赛中至少还要答对多少个题才能顺利晋级？
小明做观察水的沸腾实验，所记录的部分数据如下表：
时间/分 0 1 2 3 4 5 6 7 8
温度/℃ 20 25 30 35 40 45 50 55 60
（1）此表反映了哪两个变量之间的关系，哪个是自变量？哪个是因变量？
（2）在0-8分钟这段时间内，水的温度是怎么随着时间的变化而变化的？
（3）若时间记作t，温度记作w，请写出w和t之间的关系式．
（4）你预计第几分钟时水将沸腾（水的温度达到100℃）？
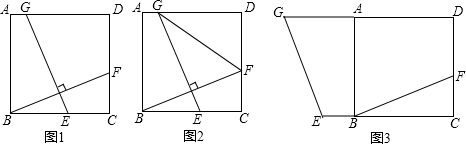
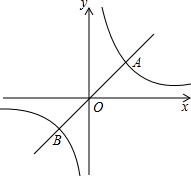如图，定义：若双曲线y=
k
x
（k＞0）与它的其中一条对称轴y=x相交于A、B两点，则线段AB的长度为双曲线y=
k
x
（k＞0）的对径．
（1）求双曲线y=
1
x
的对径．
（2）若双曲线y=
k
x
（k＞0）的对径是8
2
，求k的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网