题目内容
关于x的一元二次方程x2-2x+m-1=0有两个不相等实数根.
(1)求m的取值范围;
(2)如果x=0是方程的一个根,求m的值及方程另一个根.
(1)求m的取值范围;
(2)如果x=0是方程的一个根,求m的值及方程另一个根.
考点:根的判别式,解一元二次方程-因式分解法
专题:证明题
分析:(1)根据判别式的意义得到△=(-2)2-4(m-1)>0,然后解不等式即可;
(2)先根据方程的解的定义把x=0代入原方程求出m的值,则可确定原方程变为x2-2x=0,然后利用因式分解法解方程得到方程的另一根.
(2)先根据方程的解的定义把x=0代入原方程求出m的值,则可确定原方程变为x2-2x=0,然后利用因式分解法解方程得到方程的另一根.
解答:解:(1)根据题意得△=(-2)2-4(m-1)>0,
解得m<2;
(2)把x=0代入原方程得m-1=0,
解得m=1,
∴原方程变为x2-2x=0
解方程得x1=0,x2=2,
∴方程的另一个根为x=2.
解得m<2;
(2)把x=0代入原方程得m-1=0,
解得m=1,
∴原方程变为x2-2x=0
解方程得x1=0,x2=2,
∴方程的另一个根为x=2.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解一元二次方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若点A(a,b)在第四象限,则点(b-a,a-b)在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
 如图,抛物线y=ax2+bx-3a(a≠0)与x轴交于点A(-1,0)和点B,与y轴交于点C(0,2),连接BC.
如图,抛物线y=ax2+bx-3a(a≠0)与x轴交于点A(-1,0)和点B,与y轴交于点C(0,2),连接BC.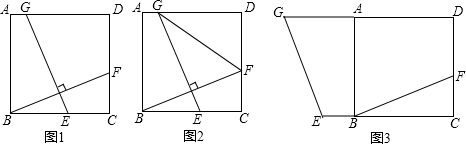
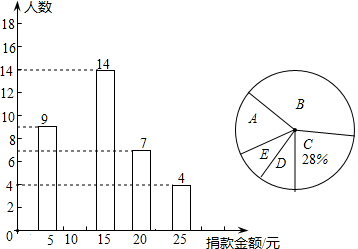 某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.
某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.