题目内容
如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BED=60°,PD=3,求PA的长.
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.

(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BED=60°,PD=3,求PA的长.
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.

考点:切线的判定,菱形的判定
专题:
分析:(1)连接OD,由AB是圆O的直径可得∠ADB=90°,进而求得∠ADO+∠PDA=90°,即可得出直线PD为⊙O的切线;
(2)求出∠P=30°,解直角三角形求出OD,根据含30°角直角三角形求出即可;
(3)根据折叠和已知求出∠P=∠PBF,根据平行线的判定推出DE∥BF,求出DF⊥AB,BE⊥AB,推出DF∥BE,求出ED=EB,根据菱形的判定推出即可.
(2)求出∠P=30°,解直角三角形求出OD,根据含30°角直角三角形求出即可;
(3)根据折叠和已知求出∠P=∠PBF,根据平行线的判定推出DE∥BF,求出DF⊥AB,BE⊥AB,推出DF∥BE,求出ED=EB,根据菱形的判定推出即可.
解答: (1)直线PD为⊙O的切线,理由是:
(1)直线PD为⊙O的切线,理由是:
如图1,连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
又∵DO=BO,
∴∠BDO=∠PBD
∵∠PDA=∠PBD,
∴∠BDO=∠PDA,
∴∠ADO+∠PDA=90°,即PD⊥OD,
∵点D在⊙O上,
∴直线PD为⊙O的切线;
(2)解:∵BE为⊙O切线,
∴∠PBE=90°,
∵∠BED=60°,
∴∠P=30°,
在Rt△PDO中,∠PDO=90°,PD=3,
∴OD=PD×tan30°=3×
=
,
∴PO=2OD=2
,
∴PA=PO-OA=2
-
=
;
(3)证明:如图2,依题意得:∠ADF=∠PDA,∠APD=∠AFD,
∵∠PDA=∠PBD,∠ADF=∠ABF,∠PAD=∠DAF,
∴∠ADF=∠AFD=∠BPD=∠ABF,
∴AD=AF,BF∥PD,
∴DF⊥PB,
∵BE为切线,
∴BE⊥PB,
∴DF∥BE,
∴四边形DFBE为平行四边形,
∵PE、BE为切线,
∴BE=DE,
∴四边形DFBE为菱形.
 (1)直线PD为⊙O的切线,理由是:
(1)直线PD为⊙O的切线,理由是:如图1,连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
又∵DO=BO,
∴∠BDO=∠PBD
∵∠PDA=∠PBD,
∴∠BDO=∠PDA,
∴∠ADO+∠PDA=90°,即PD⊥OD,
∵点D在⊙O上,
∴直线PD为⊙O的切线;
(2)解:∵BE为⊙O切线,
∴∠PBE=90°,
∵∠BED=60°,
∴∠P=30°,
在Rt△PDO中,∠PDO=90°,PD=3,
∴OD=PD×tan30°=3×
| ||
| 3 |
| 3 |
∴PO=2OD=2
| 3 |
∴PA=PO-OA=2
| 3 |
| 3 |
| 3 |
(3)证明:如图2,依题意得:∠ADF=∠PDA,∠APD=∠AFD,
∵∠PDA=∠PBD,∠ADF=∠ABF,∠PAD=∠DAF,
∴∠ADF=∠AFD=∠BPD=∠ABF,

∴AD=AF,BF∥PD,
∴DF⊥PB,
∵BE为切线,
∴BE⊥PB,
∴DF∥BE,
∴四边形DFBE为平行四边形,
∵PE、BE为切线,
∴BE=DE,
∴四边形DFBE为菱形.
点评:本题考查了切线的性质和判定,菱形的判定,平行线的判定,含30度角的直角三角形性质,解直角三角形的应用,本题是一道综合性的题目,是中档题,难度较大.

练习册系列答案
相关题目
已知关于x的一元一次方程2x+3k=x-6的解是正数,则k的取值范围是( )
| A、k>2 | B、k>-2 |
| C、k<2 | D、k<-2 |
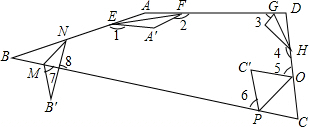 如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )
如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )| A、600° | B、700° |
| C、720° | D、800° |
代数式xy2-y2( )
| A、它是单项式 |
| B、它是x,y的积的平方与y平方的差 |
| C、它是三次二项式 |
| D、它的二次项系数为1 |
 如图,在平面直角坐标系xOy中,已知直线L1、L2都经过点A(0,5),它们分别与x轴交于点B和C,点B、C分别在x轴的负、正半轴上.
如图,在平面直角坐标系xOy中,已知直线L1、L2都经过点A(0,5),它们分别与x轴交于点B和C,点B、C分别在x轴的负、正半轴上. 如图,已知△ABC中,∠C=90°,∠A=60°,BC=6,点D是斜边AB的中点,点E在CB的延长线上,且CD=BE.求AC的长和∠E的度数.
如图,已知△ABC中,∠C=90°,∠A=60°,BC=6,点D是斜边AB的中点,点E在CB的延长线上,且CD=BE.求AC的长和∠E的度数. 如图:Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.
如图:Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动. 如图,矩形ABCD中,AB=6,BC=8,E是BC边上的一定点,P是CD边上的一动点(不与点C、D重合),M,N分别是AE、PE的中点,记MN的长度为a,在点P运动过程中,a不断变化,则a的取值范围是
如图,矩形ABCD中,AB=6,BC=8,E是BC边上的一定点,P是CD边上的一动点(不与点C、D重合),M,N分别是AE、PE的中点,记MN的长度为a,在点P运动过程中,a不断变化,则a的取值范围是